
【题目】如图,已知AB为⊙O的直径,PA是⊙O的切线,点C是⊙O上异于点A的一点,且PC=PA.
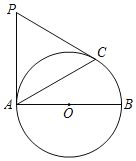
(1)求证:PC是⊙O的切线;
(2)若∠BAC=30°,AB=6,求∠P的度数及PA的长.
【答案】(1)详见解析;(2)∠P=60°, PA=3![]() .
.
【解析】
(1)连接OC,根据切线的性质得到∠PAB=90°,根据等腰三角形的性质得到∠OAC=∠OCA,再结合已知条件求得∠PCO=∠PAB=90°,从而得出PC⊥OC,根据切线的判定定理即可得到结论;
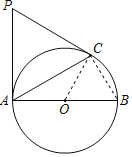
(2)连接BC,推出△PAC是等边三角形,得到∠P=60°,根据直角三角形的性质即可得到结论.
(1)连接OC,∵PA是⊙O的切线,
∴∠PAB=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∵PC=PA,
∴∠PAC=∠PCA,
∴∠PCO=∠PCA+∠ACO=∠PAC+∠OAC=∠PAB=90°,
∴PC⊥OC,,
∴PC是⊙O的切线;
(2)解:连接BC,
∵∠BAC=30°,
∴∠PAC=60°,
∵PC=PA,
∴△PAC是等边三角形,
∴∠P=60°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,AB=6,
∴AC=ABcos30°=![]() =
=![]()
∴PA=AC=![]() AB=
AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示的网格中,每个小方格都是边长为1的正方形,B点的坐标为(-1,-1).
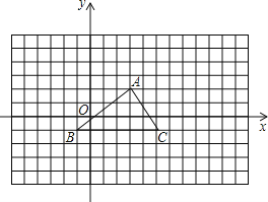
(1)把格点△ABC绕点B按逆时针方向旋转90°后得到△A1BC1,请画出△A1BC1,并写出点A1的坐标;
(2)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的相似之比为1:2,请在下面网格内画出△AB2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
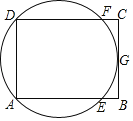
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
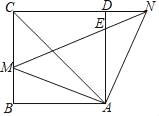
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2015年为做好“精准扶贫”,投入资金500万元用于异地安置,并规划投入资金逐年增加,2017年达到720万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)如果保持增长率不变,请你估计2019年投入资金能否突破1000万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
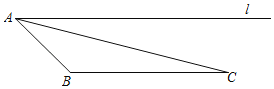
【题目】如图,在△ABC中,∠B=135°,端点为A的射线l∥CB,点A绕射线l上的某点D旋转一周所形成的图形为F,点B在图形F上.
(1)利用尺规作图确定点D的位置;
(2)判断直线BC与图形F的公共点个数,并说明理由;
(3)若AD=2,∠C=15°,求直线AC被图形F所截得的线段的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
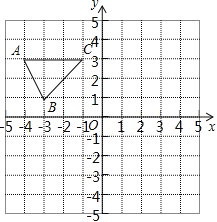
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电台“市民热线”对上周内接到的热线电话进行了分类统计,得到的统计信息图如图所示,其中有关房产城建的电话有30个,请你根据统计图的信息回答以下问题:
(1)道路交通热线电话是多少个占总数百分比是多少?
(2)上周“市民热线”接到有关环境保护方面的电话有多少个?
(3)据此估计,除环境保护方面的电话外,“市民热线”今年(按52周计算)将接到的热线电话约多少个?
(4)为了更直观显示各类“市民热线”电话的数目,你准备采用什么样的统计方法?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .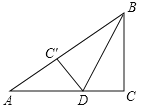
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com