
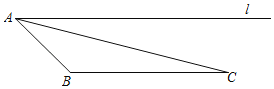
【题目】如图,在△ABC中,∠B=135°,端点为A的射线l∥CB,点A绕射线l上的某点D旋转一周所形成的图形为F,点B在图形F上.
(1)利用尺规作图确定点D的位置;
(2)判断直线BC与图形F的公共点个数,并说明理由;
(3)若AD=2,∠C=15°,求直线AC被图形F所截得的线段的长.
【答案】(1)详见解析;(2)直线BC与图形F的公共点个数为1个,理由详见解析;(3)![]() .
.
【解析】
(1)作线段AB的垂直平分线交直线l于点D,点D即为所求.
(2)直线BC与图形F的公共点个数为1个.证明DB⊥BC即可解决问题.
(3)设直线AC交⊙D于E,连接BE,作BH⊥AE于H.解直角三角形求出AH,HE即可解决问题.
解:(1)如图,点D即为所求.
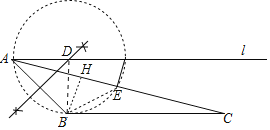
(2)直线BC与图形F的公共点个数为1个.
理由:∵直线l∥BC,
∴∠DAB+∠ABC=180°,
∵∠ABC=135°,
∴∠DAB=45°,
∵DA=DB,
∴∠DAB=∠DBA=45°,
∴∠ADB=90°,
∵∠DBC=∠ADB,
∴∠DBC=90°,
∴DB⊥BC,
∴直线BC是⊙D的切线,
∴直线BC与图形F的公共点个数为1个.
(3)设直线AC交⊙D于E,连接BE,作BH⊥AE于H.
∵AD∥BC,
∴∠DAC=∠C=15°,

∵∠DAB=45°,
∴∠BAC=45°﹣15°=30°,
∵AD=DB=2,
∴AB=![]() AD=2
AD=2![]() ,
,
∴BH=![]() AB=
AB=![]() ,AH=
,AH=![]() BH=
BH=![]() ,
,
∵∠AEB=![]() ∠ADB=45°,∠BHE=90°,
∠ADB=45°,∠BHE=90°,
∴EH=BH=![]() ,
,
∴AE=AH+BH=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:y=mx2+2mx+m﹣1(m≠0)与y轴交于点C,抛物线G的顶点为D,直线:y=mx+m﹣1(m≠0).

(1)当m=1时,画出直线和抛物线G,并直接写出直线被抛物线G截得的线段长.
(2)随着m取值的变化,判断点C,D是否都在直线上并说明理由.
(3)若直线被抛物线G截得的线段长不小于2,结合函数的图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA'的延长线恰好过点C,则sin∠ABE的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,PA是⊙O的切线,点C是⊙O上异于点A的一点,且PC=PA.
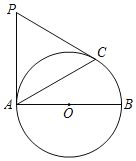
(1)求证:PC是⊙O的切线;
(2)若∠BAC=30°,AB=6,求∠P的度数及PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )
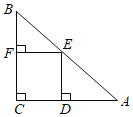
A. B.
B.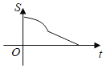 C.
C.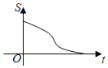 D.
D.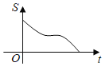
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,西藏日喀则市谢通门县发生了
日,西藏日喀则市谢通门县发生了![]() 级地震,某校九年班、九年二班两班的班长交流了为地震灾区捐款的情况:
级地震,某校九年班、九年二班两班的班长交流了为地震灾区捐款的情况:
(1)九年一班班长说:“我们班捐款总额为![]() 元,我们班人数比你们班多
元,我们班人数比你们班多![]() 人”.
人”.
(2)九年二班班长说:“我们班捐款总额也为![]() 元,我们班人均捐款比你们班人均捐款多
元,我们班人均捐款比你们班人均捐款多![]() ”.
”.
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com