
【题目】如图,抛物线![]() 经过点A(-3,0),B(1,0),C(0,-3).
经过点A(-3,0),B(1,0),C(0,-3).
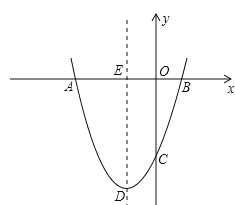
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x-3;(2)最大值![]() ,P的坐标为(-
,P的坐标为(-![]() ,-
,-![]() );(3)(0,
);(3)(0,![]() )或(0,-
)或(0,-![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).
【解析】
试题分析:(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式;
(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,x2+2x-3),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;
(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.
试题解析:(1)由于抛物线y=ax2+bx+c经过A(-3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x-1),
将C点坐标(0,-3)代入,得:
a(0+3)(0-1)=-3,解得 a=1,
则y=(x+3)(x-1)=x2+2x-3,
所以抛物线的解析式为:y=x2+2x-3;
(2)过点P作x轴的垂线,交AC于点N.
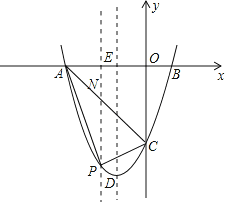
设直线AC的解析式为y=kx+m,由题意,得
![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为:y=-x-3.
设P点坐标为(x,x2+2x-3),则点N的坐标为(x,-x-3),
∴PN=PE-NE=-(x2+2x-3)+(-x-3)=-x2-3x.
∵S△PAC=S△PAN+S△PCN,
∴S=![]() PN
PN![]() OA
OA
=![]() ×3(-x2-3x)
×3(-x2-3x)
=-![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴当x=-![]() 时,S有最大值
时,S有最大值![]() ,此时点P的坐标为(-
,此时点P的坐标为(-![]() ,-
,-![]() );
);
(3)在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:
∵y=x2+2x-3=y=(x+1)2-4,
∴顶点D的坐标为(-1,-4),
∵A(-3,0),
∴AD2=(-1+3)2+(-4-0)2=20.
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图3①,
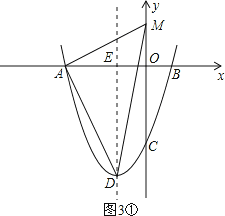
由勾股定理,得AM2+AD2=DM2,即(0+3)2+(t-0)2+20=(0+1)2+(t+4)2,
解得t=![]() ,
,
所以点M的坐标为(0,![]() );
);
②当D为直角顶点时,如图3②,
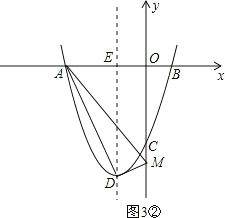
由勾股定理,得DM2+AD2=AM2,即(0+1)2+(t+4)2+20=(0+3)2+(t-0)2,
解得t=-![]() ,
,
所以点M的坐标为(0,-![]() );
);
③当M为直角顶点时,如图3③,
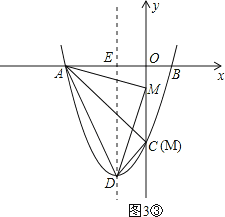
由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t-0)2+(0+1)2+(t+4)2=20,解得t=-1或-3,
所以点M的坐标为(0,-1)或(0,-3);
综上可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0,![]() )或(0,-
)或(0,-![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).


科目:初中数学 来源: 题型:
【题目】我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘船从甲码头到乙码头顺流行驶用4小时;从乙码头到甲码头逆流行驶用5小时。已知水流速度为3千米/小时,则船在静水中的平均速度是 ( )
A. 6千米/小时 B. 9千米/小时 C. 27千米/小时 D. 54千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:BF=2AD;
(2)若CE=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球半径约为6400000米,则6400000米用科学记数法表示为( )
A. 64×105米 B. 6.4×106米 C. 0.64×107米 D. 6.4×108米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com