
分析 如图,作OC⊥AB于C,连接OA、OB,利用垂径定理得到AC=BC=$\frac{1}{2}$AB=3$\sqrt{3}$,再利用勾股定理计算出OC=$\sqrt{{6}^{2}-(3\sqrt{3})^{2}}$=3,则OC=$\frac{1}{2}$OA,所以∠A=30°,则可计算出∠AOB,从而得弦AB所对的圆心角的度数.
解答 解: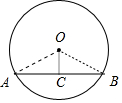 如图,作OC⊥AB于C,连接OA、OB,
如图,作OC⊥AB于C,连接OA、OB,
则AC=BC=$\frac{1}{2}$AB=3$\sqrt{3}$,
在Rt△AOC中,OC=$\sqrt{{6}^{2}-(3\sqrt{3})^{2}}$=3,
∴OC=$\frac{1}{2}$OA,
∴∠A=30°,
∴∠AOB=180°-30°-30°=120°.
∴弦AB所对的圆心角的度数为120°.
故答案为120°.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:填空题
 如图,数轴上相邻刻度之间的距离是$\frac{1}{5}$,点A表示的数是-$\frac{3}{5}$,又知点B和C表示的数互为相反数,则点B表示的有理数是-$\frac{2}{5}$.
如图,数轴上相邻刻度之间的距离是$\frac{1}{5}$,点A表示的数是-$\frac{3}{5}$,又知点B和C表示的数互为相反数,则点B表示的有理数是-$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
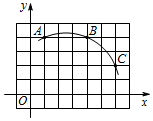 如图,在平面直角坐标系xOy中,一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),则该圆弧所在圆的圆心的坐标为($\frac{5}{2}$,$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),则该圆弧所在圆的圆心的坐标为($\frac{5}{2}$,$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com