
°æƒø°øŒ“√«—–æøπ˝µƒÕº–Œ÷–£¨‘≤µƒ»Œ∫Œ“ª∂‘∆Ω––«–œþµƒæý¿Î◊Ð «œýµ»µƒ£¨À˘“‘‘≤ «°∞µ»øÌ«˙œþ°±.≥˝¡À‘≤“‘Õ‚£¨ªπ”–“ª–©º∏∫ŒÕº–Œ“≤ «°∞µ»øÌ«˙œþ°±£¨»Á¿’¬Â»˝Ω«–Œ(»ÁÕº![]() )£¨À¸ «∑÷±“‘µ»±þ»˝Ω«–Œµƒ√ø∏ˆ∂•µ„Œ™‘≤–ƒ£¨“‘±þ≥§Œ™∞Îæ∂£¨‘⁄¡Ì¡Ω∏ˆ∂•µ„º‰ª≠“ª∂Œ‘≤ª°£¨»˝∂Œ‘≤ª°Œß≥…µƒ«˙±þ»˝Ω«–Œ. Õº
)£¨À¸ «∑÷±“‘µ»±þ»˝Ω«–Œµƒ√ø∏ˆ∂•µ„Œ™‘≤–ƒ£¨“‘±þ≥§Œ™∞Îæ∂£¨‘⁄¡Ì¡Ω∏ˆ∂•µ„º‰ª≠“ª∂Œ‘≤ª°£¨»˝∂Œ‘≤ª°Œß≥…µƒ«˙±þ»˝Ω«–Œ. Õº![]() «µ»ø̵ƒ¿’¬Â»˝Ω«–Œ∫Õ‘≤–ŒπˆƒæµƒΩÿ√ÊÕº.
«µ»ø̵ƒ¿’¬Â»˝Ω«–Œ∫Õ‘≤–ŒπˆƒæµƒΩÿ√ÊÕº.

Õº![]() Õº
Õº![]()
”–»Áœ¬Àƒ∏ˆΩ·¬€£∫
¢Ÿ¿’¬Â»˝Ω«–Œ «÷––ƒ∂‘≥∆Õº–Œ
¢⁄Õº![]() ÷–£¨µ„
÷–£¨µ„![]() µΩ
µΩ![]() …œ»Œ“‚“ªµ„µƒæý¿Î∂ºœýµ»
…œ»Œ“‚“ªµ„µƒæý¿Î∂ºœýµ»
¢€Õº![]() ÷–£¨¿’¬Â»˝Ω«–Œµƒ÷Ð≥§”Α≤µƒ÷Ð≥§œýµ»
÷–£¨¿’¬Â»˝Ω«–Œµƒ÷Ð≥§”Α≤µƒ÷Ð≥§œýµ»
¢Ð π”√Ωÿ√Ê «¿’¬Â»˝Ω«–Œµƒπˆƒæ¿¥∞·‘À∂´Œ˜£¨ª·∑¢…˙…œœ¬∂∂∂Ø
…œ ˆΩ·¬€÷–£¨À˘”–’˝»∑Ω·¬€µƒ–Ú∫≈ «£® £©
A.¢Ÿ¢⁄B.¢⁄¢€C.¢⁄¢ÐD.¢€¢Ð
°æ¥∞∏°øB
°æΩ‚Œˆ°ø
÷“ª∂‘—°œÓΩ¯––∑÷Œˆº¥ø….
¢Ÿ¿’¬Â»˝Ω«–Œ≤ª «÷––ƒ∂‘≥∆Õº–Œ£¨π ¢Ÿ¥ÌŒÛ£ª
¢⁄Õº![]() ÷–£¨µ„
÷–£¨µ„![]() µΩ
µΩ![]() …œ»Œ“‚“ªµ„µƒæý¿Î∂ºœýµ»£¨π ¢⁄’˝»∑£ª
…œ»Œ“‚“ªµ„µƒæý¿Î∂ºœýµ»£¨π ¢⁄’˝»∑£ª
¢€Õº![]() ÷–£¨…Ë‘≤µƒ∞Îæ∂Œ™r
÷–£¨…Ë‘≤µƒ∞Îæ∂Œ™r
°ý¿’¬Â»˝Ω«–Œµƒ÷Ð≥§=![]()
‘≤µƒ÷Ð≥§Œ™![]()
°ý¿’¬Â»˝Ω«–Œµƒ÷Ð≥§”Α≤µƒ÷Ð≥§œýµ»£¨π ¢€’˝»∑£ª
¢Ð π”√Ωÿ√Ê «¿’¬Â»˝Ω«–Œµƒπˆƒæ¿¥∞·‘À∂´Œ˜£¨≤ªª·∑¢…˙…œœ¬∂∂∂Ø£¨π ¢Ð¥ÌŒÛ
π —°B



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù∂˛¥Œ∫Ø ˝y£Ωax2+bx+c£®a°Ÿ0£©µƒÕºœÛ”⁄x÷·µƒΩªµ„◊¯±Í∑÷±Œ™£®x1£¨0£©£¨£®x2£¨0£©£¨«“x1£ºx2£¨ÕºœÛ…œ”–“ªµ„M£®x0£¨y0£©‘⁄x÷·œ¬∑Ω£¨∂‘”⁄“‘œ¬Àµ∑®£∫¢Ÿb2©Å4ac£æ0¢⁄x£Ωx0 «∑Ω≥Ãax2+bx+c£Ωy0µƒΩ‚¢€x1£ºx0£ºx2¢Ða£®x0©Åx1£©£®x0©Åx2£©£º0∆‰÷–’˝»∑µƒ «£®°°°°£©
A.¢Ÿ¢€¢ÐB.¢Ÿ¢⁄¢ÐC.¢Ÿ¢⁄¢€D.¢⁄¢€
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
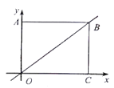
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() ”Îx÷·Ωª”⁄µ„A£®©Å1£¨0£©£¨∂•µ„◊¯±Í£®1£¨n£©£¨”Îy÷·µƒΩªµ„‘⁄£®0£¨3£©£¨£®0£¨4£©÷ƺ‰£®∞¸∫¨∂Àµ„£©£¨‘Úœ¬¡–Ω·¬€£∫¢Ÿabc£æ0£ª¢⁄3a+b£º0£ª¢€©Å
”Îx÷·Ωª”⁄µ„A£®©Å1£¨0£©£¨∂•µ„◊¯±Í£®1£¨n£©£¨”Îy÷·µƒΩªµ„‘⁄£®0£¨3£©£¨£®0£¨4£©÷ƺ‰£®∞¸∫¨∂Àµ„£©£¨‘Úœ¬¡–Ω·¬€£∫¢Ÿabc£æ0£ª¢⁄3a+b£º0£ª¢€©Å![]() °Ða°Ð©Å1£ª¢Ða+b°ðam2+bm£®mŒ™»Œ“‚ µ ˝£©£ª¢ð“ª‘™∂˛¥Œ∑Ω≥Ã
°Ða°Ð©Å1£ª¢Ða+b°ðam2+bm£®mŒ™»Œ“‚ µ ˝£©£ª¢ð“ª‘™∂˛¥Œ∑Ω≥Ã![]() ”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘£¨∆‰÷–’˝»∑µƒ”–£®°°°°£©
”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘£¨∆‰÷–’˝»∑µƒ”–£®°°°°£©

A. 2∏ˆ B. 3∏ˆ C. 4∏ˆ D. 5∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº,‘⁄÷±Ω«◊¯±Íœµ÷–,æÿ–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() ”Î◊¯±Í‘≠µ„÷ÿ∫œ,∂•µ„
”Î◊¯±Í‘≠µ„÷ÿ∫œ,∂•µ„![]() ∑÷±‘⁄◊¯±Í÷·µƒ’˝∞Î÷·…œ,
∑÷±‘⁄◊¯±Í÷·µƒ’˝∞Î÷·…œ, ![]() ,µ„
,µ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() …œ,÷±œþ
…œ,÷±œþ![]() ”Î’€œþ
”Î’€œþ![]() ”–π´π≤µ„.
”–π´π≤µ„.
£®1£©µ„![]() µƒ◊¯±Í « £ª
µƒ◊¯±Í « £ª
£®2£©»Ù÷±œþ![]() æ≠π˝µ„
æ≠π˝µ„![]() £¨«Û÷±œþ
£¨«Û÷±œþ![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®3£©∂‘”⁄“ª¥Œ∫Ø ˝![]() £¨µ±
£¨µ±![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯ºı–° ±£¨÷±Ω”–¥≥ˆ
µƒ‘ˆ¥Û∂¯ºı–° ±£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ¸º∏ƒÍπ∫ŒÔµƒ÷ß∏∂∑Ω Ω»’“Ê‘ˆ∂ý£¨ƒ≥ ˝—ß–À»§–°◊ÈæÕ¥ÀΩ¯––¡À≥È—˘µ˜≤È£¨µ˜≤ÈΩ·π˚œ‘ æ÷ß∏∂∑Ω Ω”–£∫![]() Œ¢–≈°¢
Œ¢–≈°¢![]() ÷ß∏∂±¶°¢
÷ß∏∂±¶°¢![]() œ÷Ω°¢
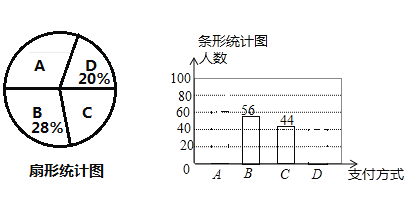
œ÷Ω°¢![]() ∆‰À˚£Æ∏√–°◊È∂‘ƒ≥≥¨ –“ªÃσ⁄π∫¬Ú’þµƒ÷ß∏∂∑Ω ΩΩ¯––µ˜≤ÈÕ≥º∆£¨µ√µΩ»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«Îƒ„∏˘æðÕ≥º∆ÕºÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
∆‰À˚£Æ∏√–°◊È∂‘ƒ≥≥¨ –“ªÃσ⁄π∫¬Ú’þµƒ÷ß∏∂∑Ω ΩΩ¯––µ˜≤ÈÕ≥º∆£¨µ√µΩ»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«Îƒ„∏˘æðÕ≥º∆ÕºÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©±æ¥Œ“ªπ≤µ˜≤È¡À √˚π∫¬Ú’þ£ø
£®2£©«Î≤π»´Ãı–ŒÕ≥º∆Õº£ª‘⁄…»–ŒÕ≥º∆Õº÷–£¨![]() ÷÷÷ß∏∂∑Ω ΩÀ˘∂‘”¶µƒ‘≤–ƒΩ«Œ™ ∂»£ª
÷÷÷ß∏∂∑Ω ΩÀ˘∂‘”¶µƒ‘≤–ƒΩ«Œ™ ∂»£ª
£®3£©»Ù∏√≥¨ –’‚“ª÷Ѓ⁄”–2000√˚π∫¬Ú’þ£¨«Îƒ„π¿º∆ π”√![]() ∫Õ
∫Õ![]() ¡Ω÷÷÷ß∏∂∑Ω Ωµƒπ∫¬Ú’þπ≤”–∂ý…Ÿ√˚£ø
¡Ω÷÷÷ß∏∂∑Ω Ωµƒπ∫¬Ú’þπ≤”–∂ý…Ÿ√˚£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∂˛¥Œ∫Ø ˝µƒ—ßœ∞÷–£¨ΩÃ≤ƒ”–»Áœ¬ƒ⁄»ð£∫
¿˝1 ∫Ø ˝ÕºœÛ«Û“ª‘™∂˛¥Œ∑Ω≥Ã![]() µƒΩ¸À∆Ω‚£®æ´»∑µΩ0.1£©£Æ
µƒΩ¸À∆Ω‚£®æ´»∑µΩ0.1£©£Æ
Ω‚£∫…Ë”–∂˛¥Œ∫Ø ˝![]() £¨¡–±Ì≤¢◊˜≥ˆÀ¸µƒÕºœÛ£®Õº1£©£Æ
£¨¡–±Ì≤¢◊˜≥ˆÀ¸µƒÕºœÛ£®Õº1£©£Æ
| °≠ |
| 0 | 1 | 2 | 3 | 4 | 5 | °≠ |
| °≠ |
|
|
|
|
|
|
| °≠ |
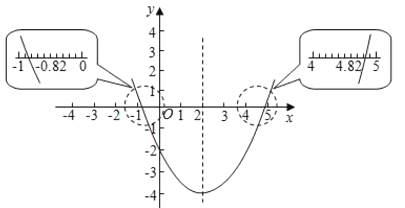
π€≤Ï≈◊ŒÔœþ∫Õ![]() ÷·Ωªµ„µƒŒª÷√£¨π¿º∆≥ˆΩªµ„µƒ∫·◊¯±Í∑÷±‘ºŒ™
÷·Ωªµ„µƒŒª÷√£¨π¿º∆≥ˆΩªµ„µƒ∫·◊¯±Í∑÷±‘ºŒ™![]() ∫Õ4.8£¨À˘“‘µ√≥ˆ∑Ω≥Ãæ´»∑µΩ0.1µƒΩ¸À∆Ω‚Œ™
∫Õ4.8£¨À˘“‘µ√≥ˆ∑Ω≥Ãæ´»∑µΩ0.1µƒΩ¸À∆Ω‚Œ™![]() £¨
£¨![]() £¨¿˚”√∂˛¥Œ∫Ø ˝
£¨¿˚”√∂˛¥Œ∫Ø ˝![]() µƒÕºœÛ«Û≥ˆ“ª‘™∂˛¥Œ∑Ω≥Ã
µƒÕºœÛ«Û≥ˆ“ª‘™∂˛¥Œ∑Ω≥Ã![]() µƒΩ‚µƒ∑Ω∑®≥∆Œ™ÕºœÛ∑®£¨’‚÷÷∑Ω∑®≥£”√¿¥«Û∑Ω≥õƒΩ¸À∆Ω‚£Æ
µƒΩ‚µƒ∑Ω∑®≥∆Œ™ÕºœÛ∑®£¨’‚÷÷∑Ω∑®≥£”√¿¥«Û∑Ω≥õƒΩ¸À∆Ω‚£Æ
–°¥œ∫Õ–°√˜Õ®π˝¿˝Ã‚µƒ—ßœ∞£¨Ãª·µΩ¿˚”√∫Ø ˝ÕºœÛø…“‘«Û≥ˆ∑Ω≥õƒΩ¸À∆Ω‚£Æ”⁄ «À˚√«≥¢ ‘¿˚”√ÕºœÛ∑®ÃΩÂ≥∑Ω≥Ã![]() µƒΩ¸À∆Ω‚£¨◊ˆ∑®»Áœ¬£∫
µƒΩ¸À∆Ω‚£¨◊ˆ∑®»Áœ¬£∫
–°¥œµƒ◊ˆ∑®£∫¡Ó∫Ø ˝![]() £¨¡–±Ì≤¢ª≠≥ˆ∫Ø ˝µƒÕºœÛ£¨ΩË÷˙ÕºœÛµ√µΩ∑Ω≥Ã
£¨¡–±Ì≤¢ª≠≥ˆ∫Ø ˝µƒÕºœÛ£¨ΩË÷˙ÕºœÛµ√µΩ∑Ω≥Ã![]() µƒΩ¸À∆Ω‚£Æ
µƒΩ¸À∆Ω‚£Æ
–°√˜µƒ◊ˆ∑®£∫“ÚŒ™![]() £¨À˘“‘œ»Ω´∑Ω≥Ã
£¨À˘“‘œ»Ω´∑Ω≥Ã![]() µƒ¡Ω±þÕ¨ ±≥˝“‘
µƒ¡Ω±þÕ¨ ±≥˝“‘![]() £¨±‰–Œµ√µΩ∑Ω≥Ã
£¨±‰–Œµ√µΩ∑Ω≥Ã![]() £¨‘Ÿ¡Ó∫Ø ˝
£¨‘Ÿ¡Ó∫Ø ˝![]() ∫Õ
∫Õ![]() £¨¡–±Ì≤¢ª≠≥ˆ’‚¡Ω∏ˆ∫Ø ˝µƒÕºœÛ£¨ΩË÷˙ÕºœÛµ√µΩ∑Ω≥Ã
£¨¡–±Ì≤¢ª≠≥ˆ’‚¡Ω∏ˆ∫Ø ˝µƒÕºœÛ£¨ΩË÷˙ÕºœÛµ√µΩ∑Ω≥Ã![]() µƒΩ¸À∆Ω‚£Æ
µƒΩ¸À∆Ω‚£Æ
«Îƒ„—°‘Ò–°¥œªÚ–°√˜µƒ◊ˆ∑®£¨«Û≥ˆ∑Ω≥Ã![]() µƒΩ¸À∆Ω‚£®æ´»∑µΩ0.1£©£Æ
µƒΩ¸À∆Ω‚£®æ´»∑µΩ0.1£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™”≠Ω”2022ƒÍ∂¨∞¬ª·£¨πƒ¿¯∏¸∂ýµƒ—ß…˙≤Œ”εΩ÷æ‘∏∑˛ŒÒ÷–¿¥£¨º◊°¢““¡ΩÀ˘—ß–£◊È÷Ø¡À÷æ‘∏∑˛ŒÒÕ≈∂”—°∞ŒªÓ∂Ø£¨æ≠π˝≥ı—°£¨¡ΩÀ˘—ß–£∏˜”–400√˚—ß…˙Ω¯»Î◊€∫œÀÿ÷ ’π æª∑Ω⁄.Œ™¡À¡ÀΩ‚¡ΩÀ˘—ß–£’‚–©—ß…˙µƒ’˚ëÈøˆ£¨¥”¡Ω–£Ω¯»À◊€∫œÀÿ÷ ’π æª∑Ω⁄µƒ—ß…˙÷–∑÷±Àʪ˙≥È»°¡À50√˚—ß…˙µƒ◊€∫œÀÿ÷ ’π æ≥…º®£®∞Ÿ∑÷÷∆£©£¨≤¢∂‘ ˝æð£®≥…º®£©Ω¯––’˚¿Ì°¢√Ë ˆ∫Õ∑÷Œˆ.œ¬√Ê∏¯≥ˆ¡À≤ø∑÷–≈œ¢.
a.º◊—ß–£—ß…˙≥…º®µƒ∆µ ˝∑÷≤º÷±∑ΩÕº»Áœ¬£® ˝æð∑÷≥…6◊È£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £©£ª
£©£ª
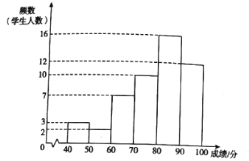
b.º◊—ß–£—ß…˙≥…º®‘⁄![]() ’‚“ª◊ȵƒ «£∫
’‚“ª◊ȵƒ «£∫
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.““—ß–£—ß…˙≥…º®µƒ∆Ωæ˘ ˝°¢÷–Œª ˝°¢÷⁄ ˝°¢”≈–„¬ £®85∑÷º∞“‘…œŒ™”≈–„£©»Áœ¬£∫
∆Ωæ˘ ˝ | ÷–Œª ˝ | ÷⁄ ˝ | ”≈–„¬ |
83.3 | 84 | 78 | 46% |
∏˘æð“‘…œ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©º◊—ß–£—ß…˙A£¨““—ß–£—ß…˙Bµƒ◊€∫œÀÿ÷ ’π æ≥…º®Õ¨Œ™83∑÷£¨’‚¡Ω»À‘⁄±æ–£—ß…˙÷–µƒ◊€∫œÀÿ÷ ’π æ≈≈√˚∏¸øø«∞µƒ «______£®ÃÓ°∞A°±ªÚ°∞B°±£©£ª
£®2£©∏˘æð…œ ˆ–≈œ¢£¨Õ∆∂œ_____—ß–£◊€∫œÀÿ÷ ’π 浃ÀÆ∆Ω∏¸∏þ£¨¿Ì”…Œ™_____£®÷¡…Ÿ¥”¡Ω∏ˆ≤ªÕ¨µƒΩ«∂»Àµ√˜Õ∆∂œµƒ∫œ¿Ì–‘£©£ª
£®3£©»Ù√øÀ˘—ß–£◊€∫œÀÿ÷ ’π 浃«∞120√˚—ß…˙Ω´±ª—°»Î÷æ‘∏∑˛ŒÒÕ≈∂”£¨‘§π¿º◊—ß–£∑÷ ˝÷¡…Ÿ¥ÔµΩ____∑÷µƒ—ß…˙≤≈ø…“‘»Î—°.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº¢Ÿ£¨‘⁄Àƒ±þ–ŒABCD÷–£¨AD°ŒBC£¨°œC=90°„£¨CD=6cm£Æ∂ص„Q¥”µ„B≥ˆ∑¢£¨“‘1cm/SµƒÀŸ∂»—ÿBC‘À∂ØµΩµ„CÕ£÷π£¨Õ¨ ±£¨∂ص„P“≤¥”Bµ„≥ˆ∑¢£¨—ÿ’€œþB°˙A°˙D‘À∂ØµΩµ„DÕ£÷𣨫“PQ°ÕBC£Æ…Ë‘À∂Ø ±º‰Œ™t£®s£©£¨µ„P‘À∂صƒ¬∑≥ÃŒ™y£®cm£©£¨‘⁄÷±Ω«◊¯±Íœµ÷–ª≠≥ˆyπÿ”⁄tµƒ∫Ø ˝ÕºœÛŒ™’€œþ∂ŒOE∫ÕEF£®»ÁÕº¢⁄£©£Æ“—÷™µ„M(4£¨5)‘⁄œþ∂ŒOE…œ£¨‘ÚÕº¢Ÿ÷–ABµƒ≥§ «________cm£Æ
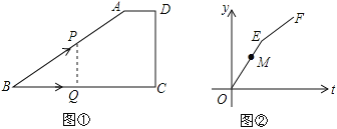
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£≥ı÷–≤ø柖– ´¥ ¥Ûª·‘§—°»¸£¨—ß–£∂‘≤Œ»¸Õ¨—ߪÒΩ±«ÈøˆΩ¯––Õ≥º∆£¨ªÊ÷∆¡À»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«ÎΩ·∫œÕº÷–œýπÿ ˝æðΩ‚¥œ¬¡–Œ £∫
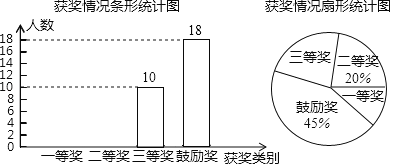
£®1£©≤Œº”¥À¥Œ ´¥ ¥Ûª·‘§—°»¸µƒÕ¨—ßπ≤”– »À£ª
£®2£©‘⁄…»–ŒÕ≥º∆Õº÷–£¨°∞»˝µ»Ω±°±À˘∂‘”¶µƒ…»–Œµƒ‘≤–ƒΩ«µƒ∂» ˝Œ™ £ª
£®3£©Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®4£©»ÙªÒµ√“ªµ»Ω±µƒÕ¨—ß÷–”–![]() ¿¥◊‘∆þƒÍº∂£¨
¿¥◊‘∆þƒÍº∂£¨![]() ¿¥◊‘æ≈ƒÍº∂£¨∆‰”ýµƒ¿¥◊‘∞ÀƒÍº∂£¨—ß–£æˆ∂®¥”ªÒµ√“ªµ»Ω±µƒÕ¨—ß÷–»Œ—°¡Ω√˚Õ¨—ß≤Œº”»´ – ´¥ ¥Ûª·±»»¸£¨«ÎÕ®π˝¡–±ÌªÚ ˜◊¥Õº∑Ω∑®«ÛÀ˘—°¡Ω√˚Õ¨—ß÷–£¨«°∫√ «“ª√˚∆þƒÍº∂∫Õ“ª√˚æ≈ƒÍº∂Õ¨—ßµƒ∏≈¬ £Æ
¿¥◊‘æ≈ƒÍº∂£¨∆‰”ýµƒ¿¥◊‘∞ÀƒÍº∂£¨—ß–£æˆ∂®¥”ªÒµ√“ªµ»Ω±µƒÕ¨—ß÷–»Œ—°¡Ω√˚Õ¨—ß≤Œº”»´ – ´¥ ¥Ûª·±»»¸£¨«ÎÕ®π˝¡–±ÌªÚ ˜◊¥Õº∑Ω∑®«ÛÀ˘—°¡Ω√˚Õ¨—ß÷–£¨«°∫√ «“ª√˚∆þƒÍº∂∫Õ“ª√˚æ≈ƒÍº∂Õ¨—ßµƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com