
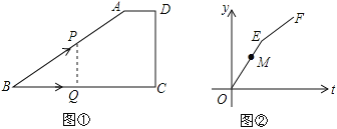
【题目】如图①,在四边形ABCD中,AD∥BC,∠C=90°,CD=6cm.动点Q从点B出发,以1cm/S的速度沿BC运动到点C停止,同时,动点P也从B点出发,沿折线B→A→D运动到点D停止,且PQ⊥BC.设运动时间为t(s),点P运动的路程为y(cm),在直角坐标系中画出y关于t的函数图象为折线段OE和EF(如图②).已知点M(4,5)在线段OE上,则图①中AB的长是________cm.
科目:初中数学 来源: 题型:
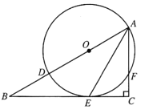
【题目】如图,△ABC内接于⊙O,AB=AC,BD为⊙O的直径,过点A作AE⊥BD于点E,延长BD交AC延长线于点F.
(1)若AE=4,AB=5,求⊙O的半径;
(2)若BD=2DF,求sin∠ACB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
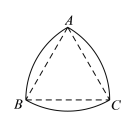
【题目】我们研究过的图形中,圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了圆以外,还有一些几何图形也是“等宽曲线”,如勒洛三角形(如图![]() ),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形. 图
),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形. 图![]() 是等宽的勒洛三角形和圆形滚木的截面图.
是等宽的勒洛三角形和圆形滚木的截面图.

图![]() 图
图![]()
有如下四个结论:
①勒洛三角形是中心对称图形
②图![]() 中,点
中,点![]() 到
到![]() 上任意一点的距离都相等
上任意一点的距离都相等
③图![]() 中,勒洛三角形的周长与圆的周长相等
中,勒洛三角形的周长与圆的周长相等
④使用截面是勒洛三角形的滚木来搬运东西,会发生上下抖动
上述结论中,所有正确结论的序号是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上,以
上,以![]() 为直径的
为直径的![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)在(1)的条件下,判断以![]() 为顶点的四边形为哪种特殊四边形,并说明理由.
为顶点的四边形为哪种特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
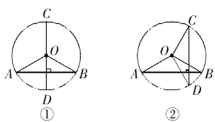
【题目】在⊙O中,AB是非直径弦,弦CD⊥AB,
(1)当CD经过圆心时(如图①),∠AOC+∠DOB=__________;
(2)当CD不经过圆心时(如图②),∠AOC+∠DOB的度数与(1)的情况相同吗?试说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求一次函数的解析式;
(2)根据图象直接写出![]() ,时
,时![]() 的取值范围;
的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:![]() . 设这种产品每天的销售利润为w元.
. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个两位数中,个位数字比十位数字大1,则称这个两位数为“递增数”.例如56就是一个“递增数”,现有2,3,4,5四个数字.
(1)若先抽出的数字3作为十位数,再从其余3个数字随机抽出1个数字为个位数,组成的两位数恰为“递增数”的概率为________.
(2)先从四个数中随机抽出一个数作为十位数,再从其余3个数字随机抽出1个数字为个位数.组成的两位数恰为“递增数”的概率是多少?请用列表或画树状图的方法分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com