
【题目】如图,△ABC内接于⊙O,AB=AC,BD为⊙O的直径,过点A作AE⊥BD于点E,延长BD交AC延长线于点F.
(1)若AE=4,AB=5,求⊙O的半径;
(2)若BD=2DF,求sin∠ACB的值.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)连接OA,在Rt△ABE中,利用勾股定理求得BE的长,设半径为![]() , 在Rt△OAE中,利用勾股定理构建方程即可求解;
, 在Rt△OAE中,利用勾股定理构建方程即可求解;
(2)连接CD,设OA交BC于点H,先证得OA⊥BC,推出OH//CD,设OH=![]() ,推出CD=
,推出CD=![]() ,OA=
,OA=![]() ,AH=
,AH=![]() ,利用勾股定理求得
,利用勾股定理求得![]() ,
,![]() ,即可求解.
,即可求解.
(1)连接OA,
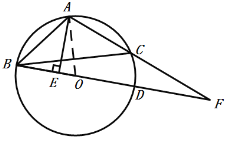
∵AE=4,AB=5,AE⊥BD,
∴![]() ,即
,即![]() ,
,
∴BE=3,
设⊙O半径为![]() ,
,
在Rt△OAE中,OA=OB=![]() ,OE=
,OE=![]() ,AE=4,
,AE=4,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴⊙O半径为![]() ;
;
(2)连接CD、OA,设OA交BC于点H,
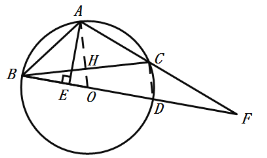
∵AB=AC,
∴![]() =
=![]() ,即点A为
,即点A为![]() 的中点,
的中点,
∴OA垂直平分BC,
∴OA⊥BC,
∵BD为直径,
∴∠BCD=90![]() ,
,
∵∠BHO=∠BCD=90![]() ,BO=OD,
,BO=OD,
∴OH//CD,CD =2OH,
设OH=![]() ,则CD=
,则CD=![]() ,
,
∵BD=2DF,
∴OD=DF,
∴CD =![]() OA,
OA,
∴OA=![]() ,
,
则AH=![]() ,
,
在Rt△BOH中,OB=OA=![]() ,OH=
,OH=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在Rt△BAH中,![]() ,
,
∴![]() ,
,
∵AB=AC,
∴sin∠ACB= ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:
的坐标定义如下:
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 的变换点
的变换点![]() 的坐标是 ;点
的坐标是 ;点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,则
,则![]() °;
°;
(2)已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .点
.点![]() 在抛物线
在抛物线上,点
![]() 的变换点为
的变换点为![]() .若点
.若点![]() 恰好在抛物线的对称轴上,且四边形
恰好在抛物线的对称轴上,且四边形![]() 是菱形,求
是菱形,求![]() 的值;
的值;
(3)若点![]() 是函数
是函数![]() 图象上的一点,点
图象上的一点,点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,以
,以![]() 为直径作
为直径作![]() ,
,![]() 的半径为
的半径为![]() ,请直接写出
,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
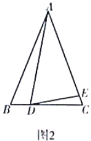
【题目】(1)问题发现
如图1,![]() 是等边三角形,点
是等边三角形,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系是 ;
之间的数量关系是 ;
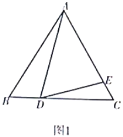
(2)拓展探究
如图2,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则(1)中的结论是否仍然成立?请说明理由.
,则(1)中的结论是否仍然成立?请说明理由.
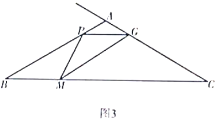
(3)解决问题
如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿
出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿![]() 方向匀速运动,同时点
方向匀速运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接
方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接![]() ,在
,在![]() 右侧作
右侧作![]() ,该角的另一边交射线
,该角的另一边交射线![]() 于点
于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
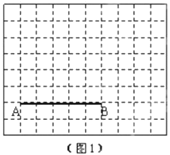
【题目】图1、图2分别是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段![]() 的两个端点均在小正方形的顶点上.
的两个端点均在小正方形的顶点上.
(1)在图1中画出以![]() 为直角边的直角
为直角边的直角![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() ;
;
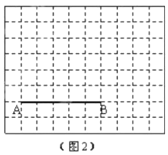
(2)在图2中画出以![]() 为腰的钝角等腰
为腰的钝角等腰![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() 的面积为10.并直接写出线段
的面积为10.并直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
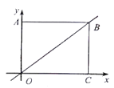
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
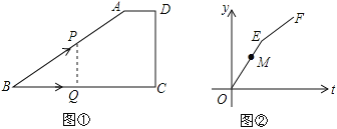
【题目】如图①,在四边形ABCD中,AD∥BC,∠C=90°,CD=6cm.动点Q从点B出发,以1cm/S的速度沿BC运动到点C停止,同时,动点P也从B点出发,沿折线B→A→D运动到点D停止,且PQ⊥BC.设运动时间为t(s),点P运动的路程为y(cm),在直角坐标系中画出y关于t的函数图象为折线段OE和EF(如图②).已知点M(4,5)在线段OE上,则图①中AB的长是________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com