
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФБфЛЛЕу
ЕФБфЛЛЕу![]() ЕФзјБъЖЈвхШчЯТЃК
ЕФзјБъЖЈвхШчЯТЃК
ЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕу![]() ЕФБфЛЛЕу
ЕФБфЛЛЕу![]() ЕФзјБъЪЧЁЁ ЁЁЃЛЕу
ЕФзјБъЪЧЁЁ ЁЁЃЛЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ЁЁ ЁЁЁуЃЛ
ЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉвбжЊХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЈЕу
ЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌЖЅЕуЮЊ
ЕФзѓВрЃЉЃЌЖЅЕуЮЊ![]() ЃЎЕу
ЃЎЕу![]() дкХзЮяЯп
дкХзЮяЯпЩЯЃЌЕу
![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЎШєЕу
ЃЎШєЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌЧѓ
ЪЧСтаЮЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєЕу![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЭМЯѓЩЯЕФвЛЕуЃЌЕу
ЭМЯѓЩЯЕФвЛЕуЃЌЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() ЃЌ
ЃЌ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈЉ3ЃЌ1ЃЉЃЛ90ЁуЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉвРОнЖдгІЕФЖЈвхПЩжБНгЕУЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЌШЛКѓвРОнЬтвтЛГіЭМаЮЃЌЙ§Еу
ЕФзјБъЃЌШЛКѓвРОнЬтвтЛГіЭМаЮЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЎНгЯТРДжЄУї
ЃЎНгЯТРДжЄУї![]() .гЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН
.гЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌШЛКѓПЩЧѓЕУ
ЃЌШЛКѓПЩЧѓЕУ![]() .
.
ЃЈ2ЃЉХзЮяЯп![]() ЕФЖЅЕуEЕФзјБъЮЊEЃЈ-2ЃЌmЃЉЃЌm>0ЃЌЩшЕуPЕФзјБъЮЊ
ЕФЖЅЕуEЕФзјБъЮЊEЃЈ-2ЃЌmЃЉЃЌm>0ЃЌЩшЕуPЕФзјБъЮЊ
![]() ЃЌЂйШє
ЃЌЂйШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ШЛКѓвРОнЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌПЩЕУЕНЙигкxКЭmЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУmЕФжЕЃЛЂкШє
ЪЧСтаЮЃЌПЩЕУЕНЙигкxКЭmЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУmЕФжЕЃЛЂкШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎЭЌРэПЩСаГіЙигкxЁЂmЕФЗНГЬзщЃЌДгЖјЧѓЕУmЕФжЕЃЛ
ЃЎЭЌРэПЩСаГіЙигкxЁЂmЕФЗНГЬзщЃЌДгЖјЧѓЕУmЕФжЕЃЛ
ЃЈ3ЃЉЩшЕуFЕФзјБъЮЊ![]() ЃЌвРОнЬтвтПЩЕУЕНЕу
ЃЌвРОнЬтвтПЩЕУЕНЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌШЛКѓвРОнСНЕуМфЕФОрРыЙЋЪНПЩЕУЕН
ЃЌШЛКѓвРОнСНЕуМфЕФОрРыЙЋЪНПЩЕУЕН![]() ЕФГЄЖШгыxЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјПЩЧѓЕУ
ЕФГЄЖШгыxЕФКЏЪ§ЙиЯЕЪНЃЌДгЖјПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЌШЛКѓПЩЧѓЕУrЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇЃЌШЛКѓПЩЧѓЕУrЕФШЁжЕЗЖЮЇ.
ЃЈ1ЃЉЁпЕу![]() ЃЌ3ЃО1ЃЌ
ЃЌ3ЃО1ЃЌ
ЁрЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() ЕФзјБъЪЧЃЈЉ3ЃЌ1ЃЉЃЎ
ЕФзјБъЪЧЃЈЉ3ЃЌ1ЃЉЃЎ
Ёп![]() ЃЌЉ4ЃМ2ЃЌ
ЃЌЉ4ЃМ2ЃЌ
ЁрЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЕФзјБъЮЊЃЈЉ2ЃЌЉ4ЃЉЃЎ
ЕФзјБъЮЊЃЈЉ2ЃЌЉ4ЃЉЃЎ
Й§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
дк![]() КЭ
КЭ![]() жа
жа ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃКЃЈЉ3ЃЌ1ЃЉЃЛ90ЁуЃЎ
ЃЈ2ЃЉгЩЬтвтЕУ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЂйШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр
Ёр![]() ЃЌЗћКЯЬтвтЁЃ
ЃЌЗћКЯЬтвтЁЃ
ЂкШє![]() ЃЌдђЕу
ЃЌдђЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁпЕу![]() ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ
ЧЁКУдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр
Ёр![]() Лђ
Лђ![]() ЃЌЗћКЯЬтвтЃЎ
ЃЌЗћКЯЬтвтЃЎ
злЩЯЫљЪіЃЌ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЩшЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌНтЕУЃК
ЪБЃЌНтЕУЃК![]() ЃЌВЛКЯЬтвтЃЎ
ЃЌВЛКЯЬтвтЃЎ
ЕБ![]() ЪБЃЌНтЕУЃК
ЪБЃЌНтЕУЃК![]() ЃЌЗћКЯЬтвтЃЎ
ЃЌЗћКЯЬтвтЃЎ
ЁпЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
Ёр ЃЎ
ЃЎ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕЃЌ
газюаЁжЕЃЌ![]() ЕФзюаЁжЕ
ЕФзюаЁжЕ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЃЌ
газюДѓжЕЃЌ![]() ЕФзюДѓжЕ
ЕФзюДѓжЕ![]() ЃЎ
ЃЎ
Ёр![]() ЕФШЁжЕЗЖЮЇЮЊЃК
ЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
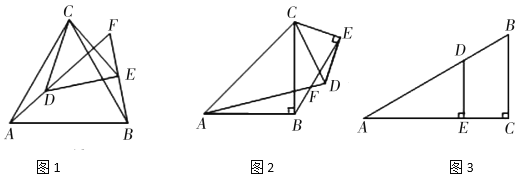
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
ШчЭМ1ЃЌ![]() КЭ
КЭ![]() ОљЮЊЕШБпШ§НЧаЮЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎ
ОљЮЊЕШБпШ§НЧаЮЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎ
ЬюПеЃКЂй![]() ЕФЖШЪ§ЪЧ____ЃЛЂкЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЮЊ________ЃЛ
ЕФЖШЪ§ЪЧ____ЃЛЂкЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЮЊ________ЃЛ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌ![]() КЭ
КЭ![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎЧыХаЖЯ
ЃЌжБЯпADКЭжБЯпBEНЛгкЕуFЃЎЧыХаЖЯ![]() ЕФЖШЪ§МАЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЌ
ЕФЖШЪ§МАЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЌ
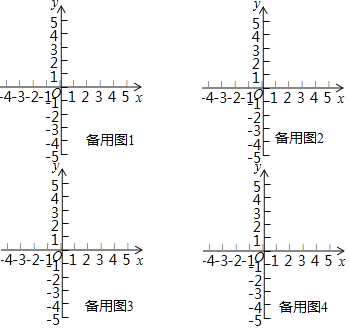
ЃЈ3ЃЉШчЭМ3ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕуDдкABБпЩЯЃЌ
ЃЌЕуDдкABБпЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦзХЕуAдкЦНУцФка§зЊЃЌЧыжБНгаДГіжБЯпDEОЙ§ЕуBЪБЃЌЕуCЕНжБЯпDEЕФОрРыЃЎ
ШЦзХЕуAдкЦНУцФка§зЊЃЌЧыжБНгаДГіжБЯпDEОЙ§ЕуBЪБЃЌЕуCЕНжБЯпDEЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
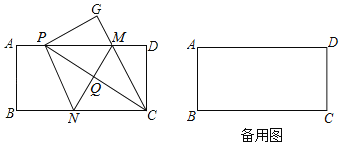
ЁОЬтФПЁПШчЭМЃЌЯжгавЛеХОиаЮжНЦЌABCDЃЌABЃН4ЃЌBCЃН8ЃЌЕуMЃЌNЗжБ№дкОиаЮЕФБпADЃЌBCЩЯЃЌНЋОиаЮжНЦЌбижБЯпMNелЕўЃЌЪЙЕуCТфдкОиаЮЕФБпADЩЯЃЌМЧЮЊЕуPЃЌЕуDТфдкGДІЃЌСЌНгPCЃЌНЛMNЖЁЕуQЃЌСЌНгCMЃЎ
ЃЈ1ЃЉЧѓжЄЃКPMЃНPNЃЛ
ЃЈ2ЃЉЕБPЃЌAжиКЯЪБЃЌЧѓMNЕФжЕЃЛ
ЃЈ3ЃЉШєЁїPQMЕФУцЛ§ЮЊSЃЌЧѓSЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНИіХњЗЂЕъЯњЪлЭЌвЛжжЦЛЙћЃЌдкМзХњЗЂЕъЃЌВЛТлвЛДЮЙКТђЪ§СПЪЧЖрЩйЃЌМлИёОљЮЊ6дЊ/![]() ЃЎдкввХњЗЂЕъЃЌвЛДЮЙКТђЪ§СПВЛГЌЙ§
ЃЎдкввХњЗЂЕъЃЌвЛДЮЙКТђЪ§СПВЛГЌЙ§![]() ЪБЃЌМлИёЮЊ7дЊ/
ЪБЃЌМлИёЮЊ7дЊ/![]() ЃЛвЛДЮЙКТђЪ§СПГЌЙ§
ЃЛвЛДЮЙКТђЪ§СПГЌЙ§![]() ЪБЃЌЦфжага
ЪБЃЌЦфжага![]() ЕФМлИёШдЮЊ7дЊ/
ЕФМлИёШдЮЊ7дЊ/![]() ЃЌГЌЙ§
ЃЌГЌЙ§![]() ВПЗжЕФМлИёЮЊ5дЊ/
ВПЗжЕФМлИёЮЊ5дЊ/![]() ЃЎЩшаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ
ЃЎЩшаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉИљОнЬтвтЬюПеЃК
ЂйШєвЛДЮЙКТђЪ§СПЮЊ![]() ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЂкШєвЛДЮЙКТђЪ§СПЮЊ![]() ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЃЈЂђЃЉЩшдкМзХњЗЂЕъЛЈЗб![]() дЊЃЌдкввХњЗЂЕъЛЈЗб
дЊЃЌдкввХњЗЂЕъЛЈЗб![]() дЊЃЌЗжБ№Чѓ
дЊЃЌЗжБ№Чѓ![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈЂѓЃЉИљОнЬтвтЬюПеЃК
ЂйШєаЁЭѕдкМзХњЗЂЕъКЭдкввХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЯрЭЌЃЌЧвЛЈЗбЯрЭЌЃЌдђЫћдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ_________![]() ЃЛ
ЃЛ
ЂкШєаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ![]() ЃЌдђЫћдкМзЁЂввСНИіХњЗЂЕъжаЕФ________ХњЗЂЕъЙКТђЛЈЗбЩйЃЛ
ЃЌдђЫћдкМзЁЂввСНИіХњЗЂЕъжаЕФ________ХњЗЂЕъЙКТђЛЈЗбЩйЃЛ
ЂлШєаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЛЈЗбСЫ260дЊЃЌдђЫћдкМзЁЂввСНИіХњЗЂЕъжаЕФ_________ХњЗЂЕъЙКТђЪ§СПЖрЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПТЬЩЋГіааЪЧЖдЛЗОГгАЯьзюаЁЕФГіааЗНЪНЃЌЁАЙВЯэЕЅГЕЁБвбГЩЮЊББОЉЕФвЛЕРіІРіЕФЗчОАЯпЃЎФГЩчЛсЪЕМљЛюЖЏаЁ
зщЮЊСЫСЫНтЁАЙВЯэЕЅГЕЁБЕФЪЙгУЧщПіЃЌЖдБОаЃНЬЪІдк3дТ6ШежС3дТ10ШеЪЙгУЕЅГЕЕФЧщПіНјааСЫЮЪОэЕїВщЃЌ
вдЯТЪЧИљОнЕїВщНсЙћЛцжЦЕФЭГМЦЭМЕФвЛВПЗжЃК
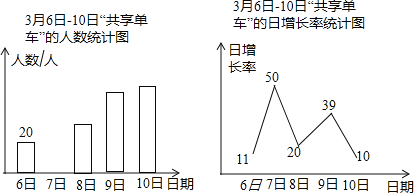
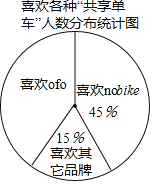
ЧыИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ3дТ7ШеЪЙгУЁАЙВЯэЕЅГЕЁБЕФНЬЪІШЫЪ§ЮЊШЫЃЌВЂЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉВЛЭЌЦЗХЦЕФЁАЙВЯэЕЅГЕЁБИїОпЬиЩЋЃЌЩчЛсЪЕМљЛюЖЏаЁзщеыЖдгаЙ§ЪЙгУЁАЙВЯэЕЅГЕЁБОРњЕФНЬЪІзіСЫНјвЛВНЕїВщЃЌУПЮЛНЬЪІЖМАДвЊЧѓбЁдёСЫвЛжжздМКЯВЛЖЕФЁАЙВЯэЕЅГЕЁБЃЌЭГМЦНсЙћШчЭМЃЌЦфжаЯВЛЖ![]() ЕФНЬЪІга36ШЫЃЌЧѓЯВЛЖ
ЕФНЬЪІга36ШЫЃЌЧѓЯВЛЖ![]() ЕФНЬЪІЕФШЫЪ§ЃЎ
ЕФНЬЪІЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
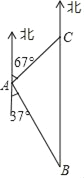
ЁОЬтФПЁПШчЭМЃЌдкИлПкAЕФФЯЦЋЖЋ37ЁуЗНЯђЕФКЃУцЩЯЃЌгавЛбВТпЭЇBЃЌAЁЂBЯрОр20КЃРяЃЌетЪБдкбВТпЭЇЕФе§ББЗНЯђМАИлПкAЕФББЦЋЖЋ67ЁуЗНЯђЩЯЃЌгавЛгцДЌCЗЂЩњЙЪеЯЃЎЕУжЊетвЛЧщПіКѓЃЌбВТпЭЇвд25КЃРя/аЁЪБЕФЫйЖШЧАЭљОШдЎЃЌЮЪбВТпЭЇФмЗёдк1аЁЪБФкЕНДягцДЌCДІЃП
ЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЌsin67ЁуЁж![]() ЃЌcos67ЁуЁж
ЃЌcos67ЁуЁж![]() ЃЌtan67ЁуЁж
ЃЌtan67ЁуЁж![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
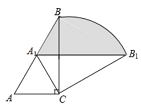
ЁОЬтФПЁПШчЭМЃЌRtЁїABC жаЃЌЁЯACBЃН90ЁуЃЌЁЯABCЃН30ЁуЃЌACЃН2ЃЌНЋЁїABCШЦЕуCЫГЪБеыа§зЊЃЌЕуAЁЂBЕФЖдгІЕуЗжБ№ЮЊA1ЁЂB1ЃЌЕБЕуA1ЧЁКУТфдкABЩЯЪБЃЌЛЁBB1гыЕуA1ЙЙГЩЕФвѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦыЦыЙўЖћЪаНЬг§ОжЯыжЊЕРФГаЃбЇЩњЖддњСњздШЛБЃЛЄЧјЕФСЫНтГЬЖШЃЌдкИУаЃЫцЛњГщШЁСЫВПЗжбЇЩњНјааЮЪОэЃЌЮЪОэгавдЯТЫФИібЁЯюЃКAЃЎЪЎЗжСЫНтЃЛBЃЎСЫНтНЯЖрЃКCЃЎСЫНтНЯЩйЃКDЃЎВЛСЫНтЃЈвЊЧѓЃКУПУћБЛЕїВщЕФбЇЩњБибЁЧвжЛФмбЁдёвЛЯюЃЉЃЎЯжНЋЕїВщЕФНсЙћЛцжЦГЩСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнСНЗљЭГМЦЭМжаЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮБЛГщШЁЕФбЇЩњЙВга_______УћЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭМЃЛ
ЃЈ3ЃЉЩШаЮЭМжаЕФбЁЯюЁАCЃЎСЫНтНЯЩйЁБВПЗжЫљеМЩШаЮЕФдВаФНЧЕФДѓаЁЮЊ_______ЁуЃЛ
ЃЈ4ЃЉШєИУаЃЙВга![]() УћбЇЩњЃЌЧыФуИљОнЩЯЪіЕїВщНсЙћЙРМЦИУаЃЖдгкдњСњздШЛБЃЛЄЧјЁАЪЎЗжСЫНтЁБКЭЁАСЫНтНЯЖрЁБЕФбЇЩњЙВгаЖрЩйУћЃП
УћбЇЩњЃЌЧыФуИљОнЩЯЪіЕїВщНсЙћЙРМЦИУаЃЖдгкдњСњздШЛБЃЛЄЧјЁАЪЎЗжСЫНтЁБКЭЁАСЫНтНЯЖрЁБЕФбЇЩњЙВгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌABЃНACЃЌBDЮЊЁбOЕФжБОЖЃЌЙ§ЕуAзїAEЁЭBDгкЕуEЃЌбгГЄBDНЛACбгГЄЯпгкЕуFЃЎ
ЃЈ1ЃЉШєAEЃН4ЃЌABЃН5ЃЌЧѓЁбOЕФАыОЖЃЛ
ЃЈ2ЃЉШєBDЃН2DFЃЌЧѓsinЁЯACBЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com