
【题目】(1)问题发现
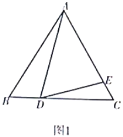
如图1,![]() 是等边三角形,点
是等边三角形,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)拓展探究
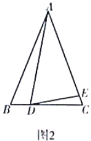
如图2,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则(1)中的结论是否仍然成立?请说明理由.
,则(1)中的结论是否仍然成立?请说明理由.
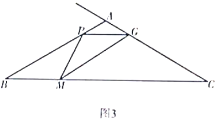
(3)解决问题
如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿
出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿![]() 方向匀速运动,同时点
方向匀速运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接
方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接![]() ,在
,在![]() 右侧作
右侧作![]() ,该角的另一边交射线
,该角的另一边交射线![]() 于点
于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)成立,见详解;(3)1或2.
;(2)成立,见详解;(3)1或2.
【解析】
(1)通过角的关系可证△ABD∽△DCE,根据相似三角形对应边成比例可得到线段的关系;
(2)同(1)中的思路相同,通过角的关系可证△ABD∽△DCE,即可得到结论;
(3)可证△PBM∽△MCG,然后得到![]() ,用
,用![]() 来表示线段的长,当G点在线段AC上时,若
来表示线段的长,当G点在线段AC上时,若![]() 为等腰三角形时,则AP=AG,代入计算即可;当G点在CA延长线上时,若
为等腰三角形时,则AP=AG,代入计算即可;当G点在CA延长线上时,若![]() 为等腰三角形时,则
为等腰三角形时,则![]() 为等边三角形,代入计算得到
为等边三角形,代入计算得到![]() .
.
(1)![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴∠B=∠C=60°,
∴∠BAD+∠ADB=180°-60°=120°,
![]() ,
,
∴∠CDE+∠ADB=180°-60°=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴![]() ;
;
(2)成立,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴∠BAD+∠ADB=![]() ,
,
∵![]() ,
,
∴∠CDE+∠ADB=![]() ,
,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴![]() ;
;
(3)∵![]() ,
,![]() ,
,
∴∠B=∠C=30°,
∴∠BPM+∠PMB=180°-30°=150°,
∵![]() ,
,
∴∠CMG+∠PMB=180°-30°=150°,
∴∠BPM=∠CMG,
又∠B=∠C=30°,
∴△PBM∽△MCG,
∴![]() ,
,
由题意可知![]() ,
,![]() ,即
,即![]() ,
,
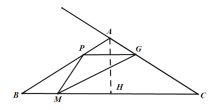
如图,过点A作AH⊥BC于H,
∵![]() ,
,![]() ,
,
∴AH=2,![]() ,
,
∵![]() ,AH⊥BC,
,AH⊥BC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
当G点在线段AC上时,若![]() 为等腰三角形时,则AP=AG,如图3,
为等腰三角形时,则AP=AG,如图3,
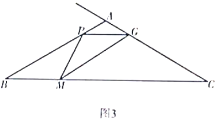
此时AG=AC-CG=![]() ,
,
∴![]() ,解得
,解得![]() ,
,
当G点在CA延长线上时,若![]() 为等腰三角形时,如下图,
为等腰三角形时,如下图,

此时∠PAG=180°-120°=60°,则![]() 为等边三角形,AP=AG,
为等边三角形,AP=AG,
此时AG=CG-AC=![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴当![]() 为等腰三角形时,
为等腰三角形时,![]() 的值为1或2.
的值为1或2.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
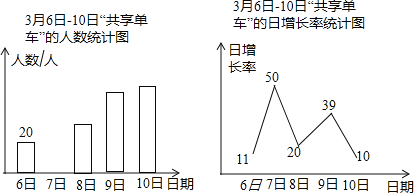
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
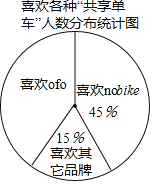
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() .
.
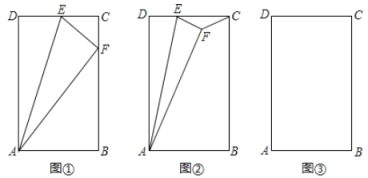
(1)如图①,点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() ∽
∽![]() ;
;
(2)如图②,点![]() 在矩形
在矩形![]() 内,连接
内,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)若以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形,则
为顶点的三角形是直角三角形,则![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当四边形![]() 是周长为20的菱形时,
是周长为20的菱形时,![]() ;
;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
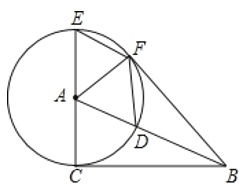
【题目】如图,△ABC内接于⊙O,AB=AC,BD为⊙O的直径,过点A作AE⊥BD于点E,延长BD交AC延长线于点F.
(1)若AE=4,AB=5,求⊙O的半径;
(2)若BD=2DF,求sin∠ACB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() ,
,![]()
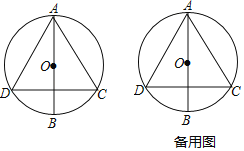
(1)求证:![]() 是等边三角形.
是等边三角形.
(2)若点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,若
,若![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() 的半径为4,点
的半径为4,点![]() 是弦
是弦![]() 的中点,点
的中点,点![]() 是直线
是直线![]() 上的任意一点,将点
上的任意一点,将点![]() 绕点
绕点![]() 逆时针旋转60°得点
逆时针旋转60°得点![]() ,求线段
,求线段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
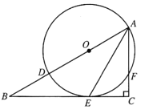
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上,以
上,以![]() 为直径的
为直径的![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)在(1)的条件下,判断以![]() 为顶点的四边形为哪种特殊四边形,并说明理由.
为顶点的四边形为哪种特殊四边形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com