
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() .
.
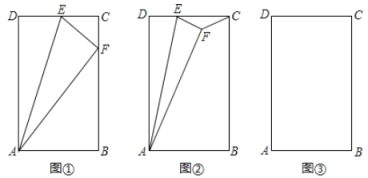
(1)如图①,点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() ∽
∽![]() ;
;
(2)如图②,点![]() 在矩形
在矩形![]() 内,连接
内,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)若以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形,则
为顶点的三角形是直角三角形,则![]() 的长为 .
的长为 .
【答案】(1)见解析;(2)![]() 的面积为
的面积为![]() ;(3)
;(3)![]() 、5、15、
、5、15、![]()
【解析】
(1)先说明∠CEF=∠AFB和![]() ,即可证明
,即可证明![]() ∽
∽![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 与点
与点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ;再结合矩形的性质,证得△FGE∽△AHF,得到AH=5GF;然后运用勾股定理求得GF的长,最后运用三角形的面积公式解答即可;
;再结合矩形的性质,证得△FGE∽△AHF,得到AH=5GF;然后运用勾股定理求得GF的长,最后运用三角形的面积公式解答即可;
(3)分点E在线段CD上和DC的延长线上两种情况,然后分别再利用勾股定进行解答即可.
(1)解:∵矩形![]() 中,
中,
∴![]()
由折叠可得![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]() ,
,![]()
∴![]() ∽
∽![]()
(2)解:过点![]() 作
作![]() 交
交![]() 与点
与点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]()
∵矩形![]() 中,
中,
∴![]()
由折叠可得:![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∴![]()
在![]() 中,
中,![]()
∵![]()
∴![]()
∴![]()
∴![]() 的面积为
的面积为![]()
(3)设DE=x,以点E、F、C为顶点的三角形是直角三角形,则:
①当点E在线段CD上时,∠DAE<45°,
∴∠AED>45°,由折叠性质得:∠AEF=∠AED>45°,
∴∠DEF=∠AED+∠AEF>90°,
∴∠CEF<90°,
∴只有∠EFC=90°或∠ECF=90°,
a,当∠EFC=90°时,如图所示:

由折叠性质可知,∠AFE=∠D=90°,
∴∠AFE+∠EFC=90°,
∴点A,F,C在同一条线上,即:点F在矩形的对角线AC上,
在Rt△ACD中,AD=5,CD=AB=3,根据勾股定理得,AC=![]() ,
,
由折叠可知知,EF=DE=x,AF=AD=5,
∴CF=AC-AF=![]() -5,
-5,
在Rt△ECF中,EF2+CF2=CE2,
∴x2+(![]() -5)2=(3-x)2,解得x=
-5)2=(3-x)2,解得x=![]() 即:DE=
即:DE=![]()
b,当∠ECF=90°时,如图所示: 点F在BC上,由折叠知,EF=DE=x,AF=AD=5,
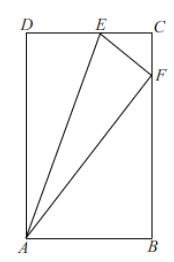
在Rt△ABF中,根据勾股定理得,BF=![]() =4,
=4,
∴CF=BC-BF=1,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
(3-x)2+12=x2,解得x=![]() ,即:DE=
,即:DE=![]() ;
;
②当点E在DC延长线上时,CF在∠AFE内部,而∠AFE=90°,
∴∠CFE<90°,
∴只有∠CEF=90°或∠ECF=90°,
a、当∠CEF=90°时,如图所示

由折叠知,AD=AF=5,∠AFE=90°=∠D=∠CEF,
∴四边形AFED是正方形,
∴DE=AF=5;
b、当∠ECF=90°时,如图所示:
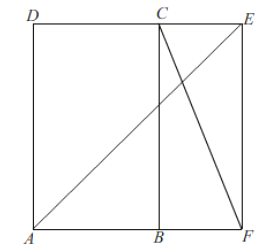
∵∠ABC=∠BCD=90°,
∴点F在CB的延长线上,
∴∠ABF=90°,由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF=![]() =4,
=4,
∴CF=BC+BF=9,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
∴(x-3)2+92=x2,解得x=15,即DE=15,
故答案为![]() 、
、![]() 、5、15.
、5、15.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
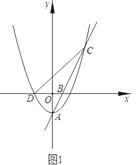
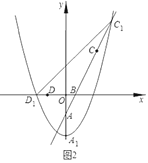
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+c(a≠0)的图象经过点B (4,0)、D (5,3),设它与x轴的另一个交点为A(点A在点B的左侧),且△ABD的面积是3.
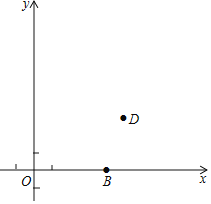
(1)求该抛物线的表达式;
(2)求∠ADB的正切值;
(3)若抛物线与y轴交于点C,直线CD交x轴于点E,点P在射线AD上,当△APE与△ABD相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9; 小亮:5,8,7,8,10,10.
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
小华 | 8 | ||
小亮 | 8 | 3 |
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,则小亮这8次射击成绩的方差 .(填“变大”、“变小”、“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
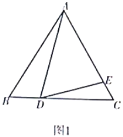
【题目】(1)问题发现
如图1,![]() 是等边三角形,点
是等边三角形,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系是 ;
之间的数量关系是 ;
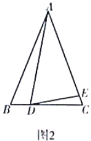
(2)拓展探究
如图2,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则(1)中的结论是否仍然成立?请说明理由.
,则(1)中的结论是否仍然成立?请说明理由.
(3)解决问题
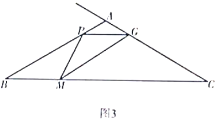
如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿
出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿![]() 方向匀速运动,同时点
方向匀速运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接
方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接![]() ,在
,在![]() 右侧作
右侧作![]() ,该角的另一边交射线
,该角的另一边交射线![]() 于点
于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有400名学生进入综合素质展示环节.为了了解两所学校这些学生的整体情况,从两校进人综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
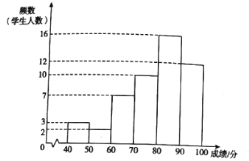
b.甲学校学生成绩在![]() 这一组的是:
这一组的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生A,乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是______(填“A”或“B”);
(2)根据上述信息,推断_____学校综合素质展示的水平更高,理由为_____(至少从两个不同的角度说明推断的合理性);
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到____分的学生才可以入选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com