
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
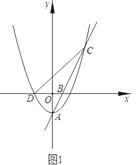
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
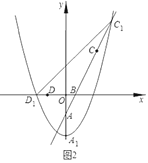
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 恒为定值
恒为定值![]() .
.
【解析】
(1)由抛物线解析式可得顶点A坐标为(0,-2),利用待定系数法即可得直线AB解析式;
(2)如图,过点![]() 作
作![]() 于
于![]() ,根据角平分线的性质可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可证明
,根据角平分线的性质可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可证明![]() ,设BE=x,BD=y,根据相似三角形的性质可得CE=2x,CD=2y,根据勾股定理由得y与x的关系式,即可用含x的代数式表示出C、D坐标,代入y=ax2-2可得关于x、a的方程组,解方程组求出a值即可得答案;
,设BE=x,BD=y,根据相似三角形的性质可得CE=2x,CD=2y,根据勾股定理由得y与x的关系式,即可用含x的代数式表示出C、D坐标,代入y=ax2-2可得关于x、a的方程组,解方程组求出a值即可得答案;
(3)过点![]() 作
作![]() 于点
于点![]() ,根据平移规律可得抛物线W1的解析式为y=
,根据平移规律可得抛物线W1的解析式为y=![]() x2-2-m,设点
x2-2-m,设点![]() 的坐标为(t,0)(t<0),代入y=
的坐标为(t,0)(t<0),代入y=![]() x2-2-m可得2+m=
x2-2-m可得2+m=![]() t2,即可的W1的解析式为y=
t2,即可的W1的解析式为y=![]() x2-
x2-![]() t2,联立直线BC解析式可用含t的代数式表示出点C1的坐标,即可得
t2,联立直线BC解析式可用含t的代数式表示出点C1的坐标,即可得![]() ,可得∠
,可得∠![]() ,根据抛物线W的解析式可得点D坐标,联立直线BC与抛物线W的解析式可得点C、A坐标,即可求出CG、DG的长,可得CG=DG,∠CDG=∠
,根据抛物线W的解析式可得点D坐标,联立直线BC与抛物线W的解析式可得点C、A坐标,即可求出CG、DG的长,可得CG=DG,∠CDG=∠![]() ,即可证明
,即可证明![]() ,可得
,可得![]() ,
,![]() ,由∠CDG=45°可得BF=DF,根据等腰三角形的性质可求出DF的长,利用勾股定理可求出CD的长,即可求出CF的长,根据三角函数的定义即可得答案.
,由∠CDG=45°可得BF=DF,根据等腰三角形的性质可求出DF的长,利用勾股定理可求出CD的长,即可求出CF的长,根据三角函数的定义即可得答案.
(1)∵抛物线W:![]() 的顶点为点
的顶点为点![]() ,
,
∴点![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∵B(1,0),
∴![]() ,
,
解得:![]() ,
,
∴抛物线解析式为:![]() .
.
(2)如图,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() 平分,
平分,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,点
,点![]() ,
,
∴点![]() ,点
,点![]() 是抛物线W:
是抛物线W:![]() 上的点,
上的点,
∴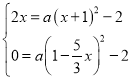 ,
,
∵x>0,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为:![]() .
.
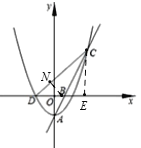
(3)![]() 恒为定值,理由如下:
恒为定值,理由如下:
如图,过点![]() 作
作![]() 轴于H,过点
轴于H,过点![]() 作
作![]() 轴G,过点
轴G,过点![]() 作
作![]() 于点
于点![]() ,
,
∵a=![]() ,
,
∴抛物线W的解析式为y=![]() x2-2,
x2-2,
∵将抛物线W向下平移m个单位,得到抛物线![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
∵抛物线![]() 与射线
与射线![]() 的交点为
的交点为![]() ,
,
∴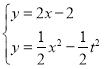 ,
,
解得: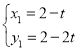 ,
, (不合题意舍去),
(不合题意舍去),
∴点![]() 的坐标
的坐标![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() 轴,
轴,
![]() ,
,
∵![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴点![]() ,
,
∵![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() ,
,
∴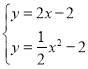 ,
,
解得:![]() 或
或![]() ,
,
∴点![]() ,A(0,-2),
,A(0,-2),
∴![]() ,
,
∴![]() ,且
,且![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() ,点
,点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 恒为定值.
恒为定值.



科目:初中数学 来源: 题型:
【题目】问题:如图1,五环图案内写有5个正整数![]() ,请对5个整数作规律探索,找出同时满足以下3个条件的数;①
,请对5个整数作规律探索,找出同时满足以下3个条件的数;①![]() 是三个连续偶数
是三个连续偶数![]() ;②
;②![]() 是两个连续奇数
是两个连续奇数![]() ;③满足
;③满足![]() .尝试: 取
.尝试: 取![]() ,如图2,
,如图2,![]() ,5个正整数满足要求;
,5个正整数满足要求;
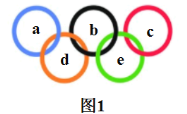
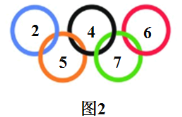
(1)取![]() ,能写出满足条件的5个正整数吗?如果能,写出
,能写出满足条件的5个正整数吗?如果能,写出![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.
(2)取![]() ,能写出满足条件的5个正整数吗?如果能,写出
,能写出满足条件的5个正整数吗?如果能,写出![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.
(3)猜想: 若5个正整数能满足上述三个要求,偶数![]() 具备怎样的条件?
具备怎样的条件?
(4)概括: 现有5个正整数![]() 满足问题中的三个条件,请用含
满足问题中的三个条件,请用含![]() 的代数式表示
的代数式表示![]() (设
(设![]() 为正整数).
为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
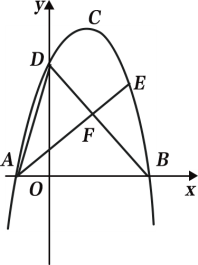
【题目】如图1,抛物线![]() 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.
(3)如图3,点M的坐标为(![]() ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
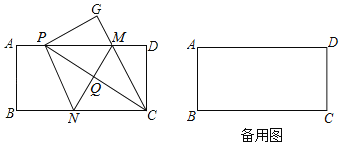
【题目】如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM.
(1)求证:PM=PN;
(2)当P,A重合时,求MN的值;
(3)若△PQM的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
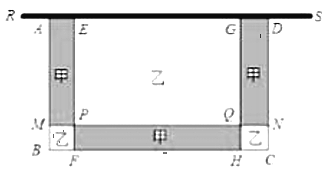
【题目】某校一面墙![]() 前有一块空地,校方准备用长
前有一块空地,校方准备用长![]() 的栅栏(
的栅栏(![]() )围成一个一面靠墙的长方形花围,再将长方形
)围成一个一面靠墙的长方形花围,再将长方形![]() 分割成六块(如图所示) ,已知
分割成六块(如图所示) ,已知![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示:
的代数式表示:![]() ;
;![]() .
.
(2)当长方形![]() 的面积等于
的面积等于![]() 时,求
时,求![]() 的长.
的长.
(3)若在如图的甲区域种植花卉.乙区域种柏草坪,种柏花卉的成本为每平方米100元,种被草坪的成本为每平方米50元,若种植花卉与草坪的总费用超过6300元,求花围的宽![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格仍为7元/
的价格仍为7元/![]() ,超过
,超过![]() 部分的价格为5元/
部分的价格为5元/![]() .设小王在同一个批发店一次购买苹果的数量为
.设小王在同一个批发店一次购买苹果的数量为![]() .
.
(Ⅰ)根据题意填空:
①若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
②若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
(Ⅱ)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小王在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的________批发店购买花费少;
,则他在甲、乙两个批发店中的________批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了260元,则他在甲、乙两个批发店中的_________批发店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
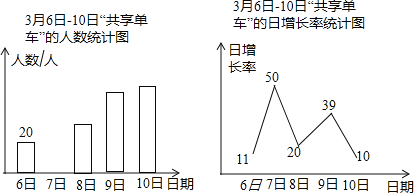
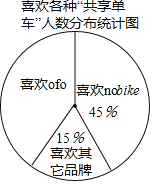
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC 中,∠ACB=90°,∠ABC=30°,AC=2,将△ABC绕点C顺时针旋转,点A、B的对应点分别为A1、B1,当点A1恰好落在AB上时,弧BB1与点A1构成的阴影部分的面积为_____.
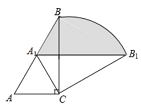
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折得
翻折得![]() .
.
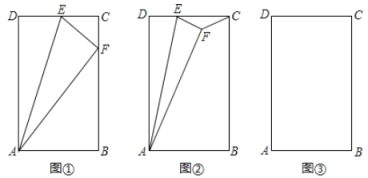
(1)如图①,点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() ∽
∽![]() ;
;
(2)如图②,点![]() 在矩形
在矩形![]() 内,连接
内,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)若以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形,则
为顶点的三角形是直角三角形,则![]() 的长为 .
的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com