
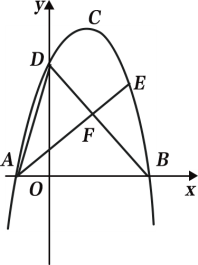
【题目】如图1,抛物线![]() 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.
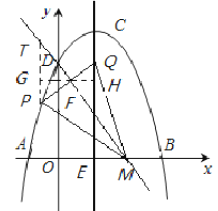
(3)如图3,点M的坐标为(![]() ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.


【答案】(1)![]() ;(2)E(2,3)或(1,4);(3)P点横坐标为
;(2)E(2,3)或(1,4);(3)P点横坐标为![]()
【解析】
(1) 抛物线![]() 的顶点为C(1,4),设抛物线的解析式为
的顶点为C(1,4),设抛物线的解析式为![]() ,由抛物线过点B,(3,0),即可求出a的值,即可求得解析式;
,由抛物线过点B,(3,0),即可求出a的值,即可求得解析式;
(2)过点E、F分别作x轴的垂线,交x轴于点M、N,设点E的坐标为![]() ,求出A、D点的坐标,得到OM=x,则AM=x+1,由AF=2EF得到
,求出A、D点的坐标,得到OM=x,则AM=x+1,由AF=2EF得到![]() ,从而推出点F的坐标
,从而推出点F的坐标![]() ,由
,由![]() ,列出关于x的方程求解即可;
,列出关于x的方程求解即可;
(3)先根据待定系数法求出直线DM的解析式为y=-2x+3,过点P作PT∥y轴交直线DM于点T,过点F作直线GH⊥y轴交PT于点G,交直线CE于点H.证明△FGP≌△FHQ,得到FG=FH,PT=![]() GH.设点P(m,-m+2m+3),则T(m,-2m+3),则PT=m-4m,GH=1-m,可得m-4m=
GH.设点P(m,-m+2m+3),则T(m,-2m+3),则PT=m-4m,GH=1-m,可得m-4m=![]() (1-m),解方程即可.
(1-m),解方程即可.
(1)∵抛物线的顶点为C(1,4),
∴设抛物线的解析式为![]() ,
,
∵抛物线过点B,(3,0),
∴![]() ,
,
解得a=-1,
∴设抛物线的解析式为![]() ,
,
即![]() ;
;
(2)如图,过点E、F分别作x轴的垂线,交x轴于点M、N,设点E的坐标为![]() ,
,

∵抛物线的解析式为![]() ,
,
当y=0时, 解得x=-1或x=3, ∴A(-1.0), ∴点D(0,3), ∴过点BD的直线解析式为 则OM=x,AM=x+1, ∴ ∴ ∴ ∴ 解得x=1或x=2, ∴点E的坐标为(2,3)或(1,4); (3)设直线DM的解析式为y=kx+b,过点D(0,3),M( 可得, 解得k=-2,b=3, ∴直线DM的解析式为y=-2x+3, ∴ ∴tan∠DMO=2, 如图,过点P作PT∥y轴交直线DM于点T,过点F作直线GH⊥y轴交PT于点G,交直线CE于点H. ∵PQ⊥MT, ∴∠TFG=∠TPF, ∴TG=2GF,GF=2PG, ∴PT= ∵PF=QF, ∴△FGP≌△FHQ, ∴FG=FH, ∴PT= 设点P(m,-m+2m+3),则T(m,-2m+3), ∴PT=m-4m,GH=1-m, ∴m-4m= 解得: ∴点P的横坐标为![]() ,
,![]() ,点F在直线BD上,
,点F在直线BD上,![]() ,
,![]() ,
,![]() ,
,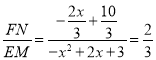 ,
,![]() ,0),
,0),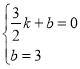 ,
,![]() ,
,![]() ,
,
![]() GF,
GF,![]() GH.
GH.![]() (1-m),
(1-m),![]() ,或
,或![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,边
的等边三角形,边![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将
出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将![]() 绕点C逆时针方向旋转60°得到
绕点C逆时针方向旋转60°得到![]() ,连接DE.
,连接DE.
(1)如图1,求证:![]() 是等边三角形;
是等边三角形;
(2)如图2,当6<t<10时,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
(3)当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数-3,1.
(1)在下列数轴上,标出表示这两个数的点,并分别用A,B表示;
(2)若|m|=2,在数轴上表示数m的点,介于点A,B之间,在A的右侧且到点B距离为5的点表示为n.
①计算m+n-mn;
②解关于x的不等式mx+4<n,并把解集表示在下列数轴上.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济宁某校为了解九年级学生艺术测试情况.以九年极(1)班学生的艺术测试成绩为样本,按![]() 、
、![]() 、
、![]() 、
、![]() 四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:![]() 级:90分~100分;
级:90分~100分;![]() 级:75分~89分;
级:75分~89分;![]() 级60分~74分;
级60分~74分;![]() 级:60分以下)
级:60分以下)
(1)此次抽样共调查了多少名学生?
(2)请求出样本中![]() 级的学生人数,井补全条形统计图;
级的学生人数,井补全条形统计图;
(3)若该校九年级有1000名学生,请你用此样本估计艺术测试中分数不低于75分的学生人数,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
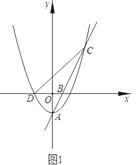
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
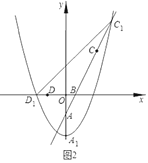
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+c(a≠0)的图象经过点B (4,0)、D (5,3),设它与x轴的另一个交点为A(点A在点B的左侧),且△ABD的面积是3.
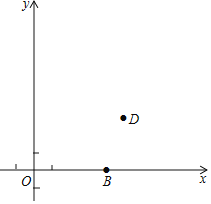
(1)求该抛物线的表达式;
(2)求∠ADB的正切值;
(3)若抛物线与y轴交于点C,直线CD交x轴于点E,点P在射线AD上,当△APE与△ABD相似时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com