
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,边
的等边三角形,边![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将
出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将![]() 绕点C逆时针方向旋转60°得到
绕点C逆时针方向旋转60°得到![]() ,连接DE.
,连接DE.
(1)如图1,求证:![]() 是等边三角形;
是等边三角形;
(2)如图2,当6<t<10时,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
(3)当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.

【答案】(1)详见解析;(2)存在,2![]() +4;(3)当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
+4;(3)当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
【解析】
试题
(1)由旋转的性质结合△ABC是等边三角形可得∠DCB=60°,CD=CE,从而可得△CDE是等边三角形;
(2)由(1)可知△CDE是等边三角形,由此可得DE=CD,因此当CD⊥AB时,CD最短,则DE最短,结合△ABC是等边三角形,AC=4即可求得此时DE=CD=![]() ;
;
(3)由题意需分0≤t<6,6<t<10和t>10三种情况讨论,①当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,由此可知:此时若△DBE是直角三角形,则∠BED=90°;②当6<t<10s时,由性质的性质可知∠DBE=120°>90°,由此可知:此时△DBE不可能是直角三角形;③当t>10s时,由旋转的性质可知,∠DBE=60°,结合∠CDE=60°可得∠BDE=∠CDE+∠BDC=60°+∠BDC>60°,由此可得∠BED<60°,由此可知此时若△BDE是直角三角形,则只能是∠BDE=90°;这样结合已知条件即可分情况求出对应的t的值了.
试题解析:
(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(2)存在,当6<t<10时,
由(1)知,△CDE是等边三角形,
∴DE=CD,
由垂线段最短可知,当CD⊥AB时,CD最小,
此时∠ADC=90°,又∵∠ACD=60°,
∴∠ACD=30°,
∴ AD=![]() AC=2,
AC=2,
∴ CD=![]() ,
,
∴ DE=2![]() (cm);
(cm);

(3)存在,理由如下:
①当0s≤t<6s时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴此时若△DBE是直角三角形,则∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEC=60°,
∴∠CEB=∠BED-∠DEC=30°,
∴∠CDA=∠CEB=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA﹣DA=6﹣4=2,
∴t=2÷1=2(s);
②当6s<t<10s时,由性质的性质可知∠DBE=120°>90°,
∴此时△DBE不可能是直角三角形;
③当t>10s时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14cm,
∴t=14÷1=14(s);
综上所述:当t=2s或14s时,以D、E、B为顶点的三角形是直角三角形.


科目:初中数学 来源: 题型:
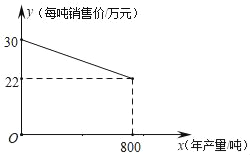
【题目】已知京润生物制品厂生产某种产品的年产量不超过800吨,生产该产品每吨所需相关费为10万元,且生产出的产品都能在当年销售完.产品每吨售价y(万元)与年产量x(吨)之间的函数关系如图所示
(1)当该产品年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣相关费用)
(2)当该产品年产量为多少吨时,该厂能获得当年销售的是大毛利润?最大毛利润多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 已知抛物线![]() 的图象经过点(-2,-1),其对称轴为x=-1.求抛物线的解析式.
的图象经过点(-2,-1),其对称轴为x=-1.求抛物线的解析式.
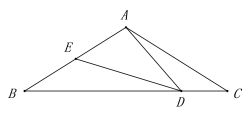
(2) 如图,在△ABC中,AB=AC,点D,E分别是BC,AB边上的点,且∠ADE=∠C.
求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若干间住房,住宿记录提供了如下信息:
(1)4月17日全部住满,一天住宿费收入为12000元;
(2)4月18日有20间房空着,一天住宿费收入为9600元;
(3)该宾馆每间房每天收费标准相同.
①一个分式方程,求解该宾馆共有多少间住房,每间住房每天收费多少元?
②通过市场调查发现,每间住房每天的定价每增加10元,就会有5个房间空闲;已知该宾馆空闲房间每天每间支出费用10元,有顾客居住房间每天每间支出费用20元,问房价定为多少元时,该宾馆一天的利润为11000元?(利润=住宿费收入﹣支出费用)
③在(2)的计算基础上,你能发现房价定为多少元时,该宾馆一天的利润最大?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
, ![]() 上,将纸片
上,将纸片![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在
落在![]() 上的一点
上的一点![]() 处,点
处,点![]() 落在点
落在点![]() 处,有以下四个结论:
处,有以下四个结论:
①四边形![]() 是菱形;②
是菱形;②![]() 平分
平分![]() ;③线段
;③线段![]() 的取值范围为
的取值范围为![]() ;④当点
;④当点![]() 与点
与点![]() 重合时,
重合时,![]() .
.
以上结论中,你认为正确的有( )个.
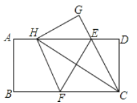
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO
(1)当∠BCO=25°时,求∠A的度数;
(2)若CD=4![]() ,BE=4,求⊙O的半径.
,BE=4,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
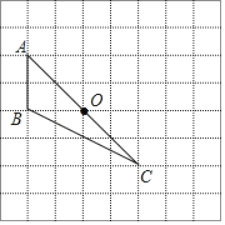
【题目】如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1.在网格中画出△A1B1C1;
(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距240千米,甲、两车沿同一线路从A地出发到B地,分别以一定的速度匀速行驶,甲先出发40分钟,乙车才出发,途中乙车发生故障,修车耗时20分钟,随后乙车车速比发生故障前减少了a千米/小时(仍保持匀速行驶),甲、乙两车同时到达B地,甲、乙两车相距的路程y(千米)与甲车行驶时间x(小时)之间的关系如图所示,则a的值为____.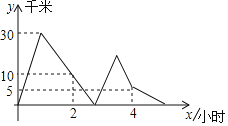
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com