
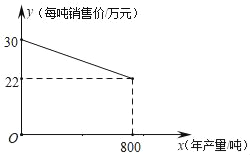
����Ŀ����֪����������Ʒ������ij�ֲ�Ʒ�������������800�֣������ò�Ʒÿ��������ط�Ϊ10��Ԫ�����������IJ�Ʒ�����ڵ��������꣮��Ʒÿ���ۼ�y����Ԫ���������x���֣�֮��ĺ�����ϵ��ͼ��ʾ
��1�����ò�Ʒ�����Ϊ���ٶ�ʱ������ɻ��7500��Ԫë����ë�������۶��ط��ã�
��2�����ò�Ʒ�����Ϊ���ٶ�ʱ���ó��ܻ�õ������۵��Ǵ�ë�������ë���������Ԫ��
���𰸡���1�����ò�Ʒ�����Ϊ500��ʱ������ɻ��7500��Ԫë����2�����ò�Ʒ�����Ϊ800��ʱ���ó��ܻ�õ������۵����ë�������ë������9600��Ԫ��
��������
��1���������������ò�Ʒÿ���ۼ�y����Ԫ���������x���֣�֮��ĺ�����ϵʽ���Ӷ������г���Ӧ�ķ��̣�������Խ����
��2����������ͣ�1���еĺ�����ϵʽ��������õ��ò�Ʒ�����Ϊ���ٶ�ʱ���ó��ܻ�õ������۵����ë�������ë���������Ԫ��
��1�����Ʒÿ���ۼ�y����Ԫ���������x���֣�֮��ĺ�����ϵ��y��ax+b��
��![]() ����
����![]() ��
��
��y����0.01x+30��
����0.01x+30��x��10x��7500��
��ã�x1��500��x2��1500����ȥ����
�𣺵��ò�Ʒ�����Ϊ500��ʱ������ɻ��7500��Ԫë����
��2����ó��ܻ�õ������۵�ë����Ϊw��Ԫ��
w������0.01x+30��x��10x����0.01��x��1000��2+10000��
��0��x��800��
�൱x��800ʱ��wȡ�����ֵ����ʱw��9600��
�𣺵��ò�Ʒ�����Ϊ800��ʱ���ó��ܻ�õ������۵����ë�������ë������9600��Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����(2)����֯��һ�ξ����ж��������ס������Ӹ�10�˵ı����ɼ����±�(10����)��
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)�ӳɼ�����λ���� �֣��Ҷӳɼ��������� �֣�
(2)�����Ҷӵ�ƽ���ɼ��ͷ��
(3)��֪�ӳɼ��ķ�����1.4����ɼ���Ϊ������� �ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC���ڽ�ƽ���������ƽ���߷ֱ�BC��BC���ӳ����ڵ�P��Q��
��1������PAQ�Ĵ�С��
��2������MΪPQ���е㣬��֤��PM2��CM��BM��
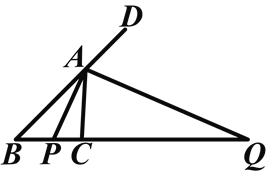
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
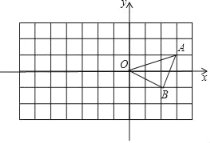
����Ŀ������ֽ��ÿ��С�����εı߳����ǵ�λ1����OAB��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��������⣺
��1���밴Ҫ��ԡ�OAB���任���Ե�OΪλ�����ģ�λ�Ʊ�Ϊ2��1������ABC��λ�����ĵ������зŴ�õ���OA��B�䣮
��2��д����A������ꣻ
��3�����OA��B'�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
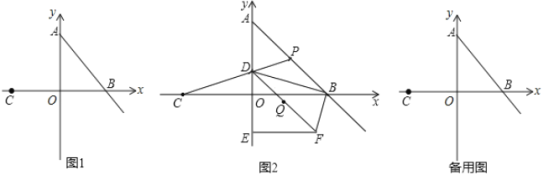
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
��1����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����ͼ2����![]() ���߶�
���߶�![]() ��������
��������![]() ��
��![]() ���㣩�ϣ�����
���㣩�ϣ�����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �Ĵ�ֱƽ���߽��ڵ�
�Ĵ�ֱƽ���߽��ڵ�![]() ������
������![]() ���ӳ�����
���ӳ�����![]() ��ʹ
��ʹ![]() ����
����![]() ����
����![]() ������
������![]() ����֤��
����֤��![]() ��
��
��3���ڣ�2���������£���![]() �ı�
�ı�![]() ʱ�����
ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
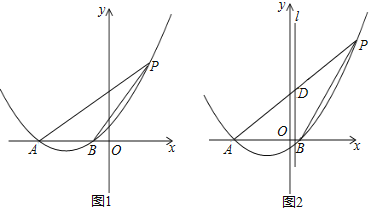
������![]() ��ֱ��l�����ĶԳ��ᣬ�Ѹ�����������x��ˮƽ����ƽ��
��ֱ��l�����ĶԳ��ᣬ�Ѹ�����������x��ˮƽ����ƽ��![]() ����λ���Ⱥ���x�ύ�ڵ�A��B��
����λ���Ⱥ���x�ύ�ڵ�A��B��![]() ��B�����
��B�����![]() ����ͼ1��PΪƽ�ƺ����������λ�ڵ�һ�����ڵ�һ��
����ͼ1��PΪƽ�ƺ����������λ�ڵ�һ�����ڵ�һ��
![]() ��A������Ϊ______��
��A������Ϊ______��
![]() ����P�ĺ�����Ϊ
����P�ĺ�����Ϊ![]() �������mΪ��ֵʱ
�������mΪ��ֵʱ![]() �����������������ֵ��
�����������������ֵ��
![]() ��ͼ2��AP��l�ڵ�D����DΪAP���е�ʱ����֤��
��ͼ2��AP��l�ڵ�D����DΪAP���е�ʱ����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
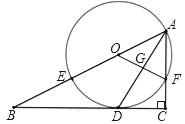
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬ADƽ����BAC��BC�ڵ�D��OΪAB��һ�㣬������A��D����O�ֱ�AB��AC�ڵ�E��F������OF��AD�ڵ�G��
(1)��֤��BC����O�����ߣ�
(2)��AB=x��AF=y�����ú�x��y�Ĵ���ʽ��ʾ�߶�AD�ij���
(3)��BE=8��sinB=![]() ����DG�ij���
����DG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����һ����Ϸ�����Ŵ�С���ʵض���ͬ�Ŀ�Ƭ�Ϸֱ��������2��3��4(������ȫ��ͬ)���ֽ��������ֵ�һ�泯����С�����������ȡһ�����������ֺ�Ż�ϴ����Ȼ��С�����������ȡһ��������С����С����õ���������֮��������Ϊ��������С��ʤ������Ϊż������С��ʤ��
(1)�����û���״ͼ���б��ķ����������������Ϊ6�ĸ�����
(2)����Ϊ�����Ϸ�����˫����ƽ��˵˵���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �ĵȱ������Σ���
�ĵȱ������Σ���![]() ������
������![]() �ϣ���
�ϣ���![]() ����
����![]() �ӵ�
�ӵ�![]() ��������OM�ķ�����1cm/s���ٶ��˶�����D�����A�غ�ʱ����
��������OM�ķ�����1cm/s���ٶ��˶�����D�����A�غ�ʱ����![]() �Ƶ�C��ʱ�뷽����ת60���õ�
�Ƶ�C��ʱ�뷽����ת60���õ�![]() ������DE.
������DE.
��1����ͼ1����֤��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��2����ͼ2����6<t<10ʱ��DE�Ƿ������Сֵ�������ڣ����DE����Сֵ���������ڣ���˵������.
��3������D������OM���˶�ʱ���Ƿ������D��E��BΪ�������������ֱ�������Σ������ڣ������ʱt��ֵ���������ڣ���˵������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com