
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() ,
,![]()
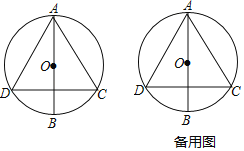
(1)求证:![]() 是等边三角形.
是等边三角形.
(2)若点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,若
,若![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() 的半径为4,点
的半径为4,点![]() 是弦
是弦![]() 的中点,点
的中点,点![]() 是直线
是直线![]() 上的任意一点,将点
上的任意一点,将点![]() 绕点
绕点![]() 逆时针旋转60°得点
逆时针旋转60°得点![]() ,求线段
,求线段![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用垂径定理的推论证明AB垂直平分DC,得到AD=AC,再证明∠DAC=60°即可推出△ACD是等边三角形;
(2)连接OC,OE,先证明∠OCF=90°,再求出半径OC的长.在Rt△OCF中通过勾股定理即可求出OF的长;
(3)先判断点P'的轨迹是直线DB,过点Q作QP'⊥DB于点P',则QP'的值最小,连接DQ,再求出DQ的长度.解Rt△QDP'即可得出结论.
(1)如图1.
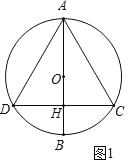
设AB与DC交点为H.
∵AB是⊙O的直径,CD⊥AB,∴DH=CH,![]() ,
,![]() ,∴AD=AC,∠CAB=∠DAB=30°,∴∠DAC=60°,∴△ACD是等边三角形;
,∴AD=AC,∠CAB=∠DAB=30°,∴∠DAC=60°,∴△ACD是等边三角形;
(2)如图2,连接OC,OE.
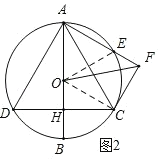
∵△ACD是等边三角形,∴∠D=60°,∴∠AOC=2∠D=120°.
∵∠CAB=30°,∴∠HOC=60°.
∵E为![]() 中点,∴
中点,∴![]() ,∴∠EOC=∠EOA
,∴∠EOC=∠EOA![]() 120°=60°,∴∠EAC
120°=60°,∴∠EAC![]() ∠EOC=30°.在Rt△ACF中,∵CF=2,∠EAC=30°,∴AC=4,∠ACF=60°,∴∠OCF=∠OCA+∠ACF=90°,∴DC=AC=4,∴CH
∠EOC=30°.在Rt△ACF中,∵CF=2,∠EAC=30°,∴AC=4,∠ACF=60°,∴∠OCF=∠OCA+∠ACF=90°,∴DC=AC=4,∴CH![]() DC=2.在Rt△OHC中,∵∠HOC=60°,∠OCH=30°,∴OC=2
DC=2.在Rt△OHC中,∵∠HOC=60°,∠OCH=30°,∴OC=2![]() .在Rt△OCF中,OF
.在Rt△OCF中,OF![]() ;
;
(3)如图3,随着点P的运动,点P'的轨迹为直线DB,过点Q作QP'⊥DB于点P',则QP'的值最小,连接DQ.

∵Q为AC中点,∴AQ=CQ![]() AC,∠ADQ=∠CDQ
AC,∠ADQ=∠CDQ![]() ∠ADC=30°,∴∠OCH=30°.在Rt△OCH中,OC=4,∴HC=4
∠ADC=30°,∴∠OCH=30°.在Rt△OCH中,OC=4,∴HC=4![]() 2
2![]() ,∴DC=4
,∴DC=4![]() .在Rt△DCQ中,∠DCQ=60°,∴DQ=4
.在Rt△DCQ中,∠DCQ=60°,∴DQ=4![]() 6.在Rt△QDP'中,∠QDP'=90°﹣∠ADQ=60°,∴QP'=6
6.在Rt△QDP'中,∠QDP'=90°﹣∠ADQ=60°,∴QP'=6![]() 3
3![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+c(a≠0)的图象经过点B (4,0)、D (5,3),设它与x轴的另一个交点为A(点A在点B的左侧),且△ABD的面积是3.
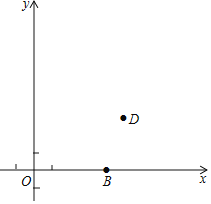
(1)求该抛物线的表达式;
(2)求∠ADB的正切值;
(3)若抛物线与y轴交于点C,直线CD交x轴于点E,点P在射线AD上,当△APE与△ABD相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
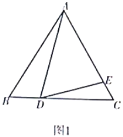
如图1,![]() 是等边三角形,点
是等边三角形,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)拓展探究
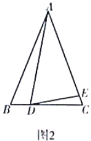
如图2,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.若
上.若![]() ,则(1)中的结论是否仍然成立?请说明理由.
,则(1)中的结论是否仍然成立?请说明理由.
(3)解决问题
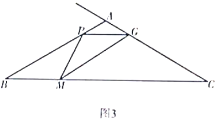
如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿
出发,以img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/25/16/9b7a314d/SYS202005251646204964745826_ST/SYS202005251646204964745826_ST.021.png" width="47" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />的速度沿![]() 方向匀速运动,同时点
方向匀速运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接
方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动.连接![]() ,在
,在![]() 右侧作
右侧作![]() ,该角的另一边交射线
,该角的另一边交射线![]() 于点
于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
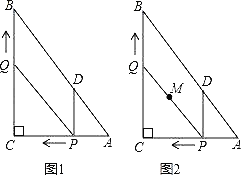
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
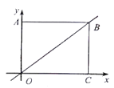
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示支付方式有:![]() 微信、
微信、![]() 支付宝、
支付宝、![]() 现金、
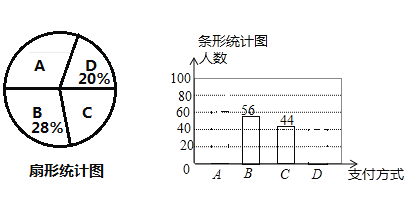
现金、![]() 其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 名购买者?
(2)请补全条形统计图;在扇形统计图中,![]() 种支付方式所对应的圆心角为 度;
种支付方式所对应的圆心角为 度;
(3)若该超市这一周内有2000名购买者,请你估计使用![]() 和
和![]() 两种支付方式的购买者共有多少名?
两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有400名学生进入综合素质展示环节.为了了解两所学校这些学生的整体情况,从两校进人综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
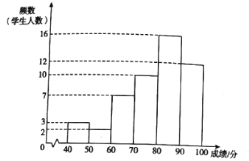
b.甲学校学生成绩在![]() 这一组的是:
这一组的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生A,乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是______(填“A”或“B”);
(2)根据上述信息,推断_____学校综合素质展示的水平更高,理由为_____(至少从两个不同的角度说明推断的合理性);
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到____分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com