
【题目】如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1 .

(1)写出点D1的坐标________;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2(4,5),画出平移后的图形;
(3)求点D旋转到点D1所经过的路线长.
科目:初中数学 来源: 题型:
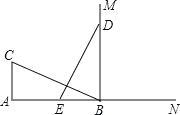
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接安顺市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
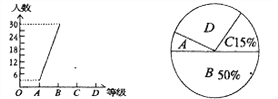
(2)补全折线统计图;
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________;
(4)若等级A为优秀,求该班的优秀率.
【答案】(1)60;(2)补图见解析;(3)108°;(4)5%.
【解析】(1)用B等人数除以其所占的百分比即可得到总人数;
(2)用求得的总人数乘以C等所占的百分比即可得到C等的人数,总人数减去A、C等的人数即可求得D等的人数;
(3)用D等的人数除以总人数乘以360°即可得到答案;
(4)用A等的人数除以总人数乘以100%即可得到答案. 解答:
解:(1)30÷50%=60(人)
∴八年级一共有60人。
(2)等级为“C”的人数为60×15%=9(人).
等级为“D”的人数为603309=18(人).
补全折线统计图如下。
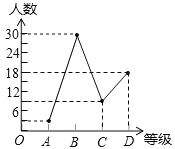
(3)等极为“D”的部分所占圆心角的度数为![]() ×360°=108°,
×360°=108°,
故答案为:108°.
(4)该班的优秀率![]() ×100%=5%.
×100%=5%.
∴该班的优秀率为5%.
点睛:本题考查统计相关知识.利用拆线图与扇形图得出相关信息是解题的关键.
【题型】解答题
【结束】
25
【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴.
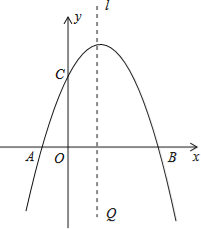
(1)求抛物线的函数关系式;
(2)求抛物线的顶点坐标;
(3)设P点是直线L上的一个动点,当△PAC的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进45件A商品和20件B商品共用了800元,购进60件A商品和35件B商品共用了1100元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购进B商品的件数比购进A商品件数的2倍少4件,如果需要购进A、B两种商品的总件数不少于32件,且该商店购进A、B两种商品的总费用不超过296元,那么该商店有几种购进方案?并写出所有可能的购进方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题:

(1)请补全统计图;
(2)在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是________度;
(3)该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
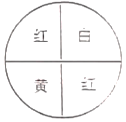
【题目】如图,小华蒙上眼睛投飞镖且中目标(转盘技等分成4个扇形,投在边线上忽略)(直接填写答案)
(1)击中红色区域的概率是 .
(2)击中白色区域的概率是 .
(3)没有击中黄色区域的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是∠
是∠![]() 内的一点,过点
内的一点,过点![]() 作
作![]() 于点
于点![]() 于点
于点![]() ,且
,且![]() .
.
![]() 求证:
求证: ![]() ;
;
![]() 如图②,点
如图②,点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,若
,若![]() .求线段
.求线段![]() 的长.
的长.
![]() 如图③,若
如图③,若![]() ,将
,将![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,![]() 秒后,
秒后,![]() 开始绕点
开始绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,![]() 旋转
旋转![]() 后停止,此时
后停止,此时![]() 也随之停止旋转。旋转过程中,
也随之停止旋转。旋转过程中,![]() 所在直线与
所在直线与![]() 所在直线的交点记为
所在直线的交点记为![]() 所在直线与
所在直线与![]() 所在直线的交点记为
所在直线的交点记为![]() .问
.问![]() 旋转几秒时,
旋转几秒时,![]() ?
?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com