
分析 (1)用加减消元法或代入法先把三元一次方程组化为二元一次方程组再求解.
(2)根据同底数幂的除法,可得要求的形式,根据幂的乘方,可得答案.
解答 解:(1)$\left\{\begin{array}{l}{2x+y+z=-1①}\\{3y-z=-1②}\\{3x+2y+3z=-5③}\end{array}\right.$
由②得z=3y+1④,
把z=3y+1分别代入①③得$\left\{\begin{array}{l}{2x+4y=-2}\\{3x+11y=-8}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$
把y=-1代入④得z=-2,
∴原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=-2}\end{array}\right.$.
(2)a2x-y=a2x÷ay
=(ax)2÷ay
=102÷2
=50.
点评 本题考查了解三元一次方程组,同底数幂的乘方以及同底数幂的除法;解三元一次方程组关键是先把三元一次方程组化为二元一次方程组,再用解二元一次方程组的知识求解.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
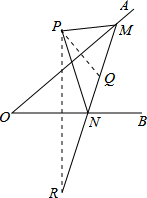 如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为4.5cm.
如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为4.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
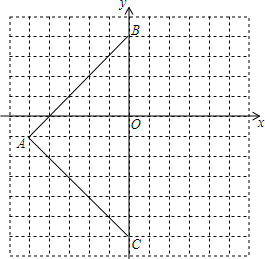 如图,三角形ABC在平面直角坐标系中,三个顶点坐标分别为A(-5,-1)、B(0,4)、C(0,-6).
如图,三角形ABC在平面直角坐标系中,三个顶点坐标分别为A(-5,-1)、B(0,4)、C(0,-6).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
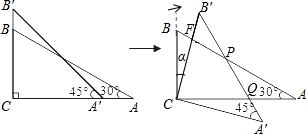 如图所示,∠C=90°,Rt△ABC中,∠A=30°,Rt△A′B′C中,∠A=45°,点A′、B分别在线段AC、B′C上.将△A′B′C绕直角顶点C顺时针旋转一个锐角α时,边A′B′分别交AB、AC于P、Q,且△APQ为等腰三角形,则锐角α的度数15°.
如图所示,∠C=90°,Rt△ABC中,∠A=30°,Rt△A′B′C中,∠A=45°,点A′、B分别在线段AC、B′C上.将△A′B′C绕直角顶点C顺时针旋转一个锐角α时,边A′B′分别交AB、AC于P、Q,且△APQ为等腰三角形,则锐角α的度数15°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com