
【题目】在平面中,给定线段AB和C,P两点,点C与点P分布在线段AB的异侧,满足![]() ,则称点C与点P是关于线段AB的关联点.在平面直角坐标系xOy中,已知点
,则称点C与点P是关于线段AB的关联点.在平面直角坐标系xOy中,已知点![]() ,
,![]() ,
,![]() .
.
(1)在![]() ,
,![]() ,
,![]() 三个点中,点O与点P是关于线段AB的关联点的是________;
三个点中,点O与点P是关于线段AB的关联点的是________;
(2)若点C与点P是关于线段OA的关联点,求点P的纵坐标m的取值范围;
(3)直线![]() 与x轴,y轴分别交与点E,F,若在线段AB上存在点P与点O是关于线段EF的关联点,直接写出b的取值范围.
与x轴,y轴分别交与点E,F,若在线段AB上存在点P与点O是关于线段EF的关联点,直接写出b的取值范围.
【答案】(1)P1, P3;(2)-![]() ≤m<0;(3)1≤b<2
≤m<0;(3)1≤b<2
【解析】
(1)分别求出∠AP1B,∠AP2B,∠AP3B,当所求角等于90°时即为点O的关联点;
(2)根据题意确定点O、A、C、P四边共圆,故点P在劣弧OA上,当CP是直径时,存在m的最小值,利用勾股定理求出半径AE,即可得到PD,由此求出m的最小值,得到m的取值范围;
(3)求出直线AB的解析式为y=-x+2,证明直线![]() 与直线AB平行,当以EF为直径的圆与直线AB相切时有最小值,与直线AB相交时都可得到∠EPF=90°,故b<2,求出以EF为直径的圆与直线AB相切时FP=OF=BF=1,由此得到b的取值范围.
与直线AB平行,当以EF为直径的圆与直线AB相切时有最小值,与直线AB相交时都可得到∠EPF=90°,故b<2,求出以EF为直径的圆与直线AB相切时FP=OF=BF=1,由此得到b的取值范围.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴∠AP1B=90°,
∴∠AOB+∠AP1B=180°,
∴点O与点P1是关于线段AB的关联点;
∵![]() ,
,
∴![]() ,
, ![]()
∴![]() ,
,
∴![]() ,故点O与点P2不是关于线段AB的关联点;
,故点O与点P2不是关于线段AB的关联点;
∵![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴∠AOB+∠AP3B=180°,
∴点O与点P3是关于线段AB的关联点;
故答案为:P1、P3;
(2) ∵点C与点P是关于线段OA的关联点,
∴点O、A、C、P四边共圆,故点P在劣弧OA上,当CP是直径时,存在m的最小值,
设圆心为E,
∵![]() ,A(2,0),
,A(2,0),
∴CP⊥OA,CD=![]() ,OD=AD=1,
,OD=AD=1,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴PD=![]() ,即m=-
,即m=-![]() ,
,
∴-![]() ≤m<0 ;
≤m<0 ;

(3)设直线AB的解析式为y=mx+n,将点A(2,0),B(0,2)代入,得
![]() ,∴
,∴![]() ,
,
∴直线AB的解析式为y=-x+2,
∴直线![]() 与直线AB平行,
与直线AB平行,
∵A(2,0),B(0,2),
∴OA=OB,
∴∠OFE=∠OBA=45°,
∵∠EOF=90°,点P与点O是关于线段EF的关联点,
∴∠EPF=90°,
∴当以EF为直径的圆与直线AB相切时有最小值,与直线AB相交时都可得到∠EPF=90°,故b<2,
当以EF为直径的圆与直线AB相切时,连接EF中点N与点P,连接PE、PF,
∴∠BPN=90°,
∴∠FNP=90°,
∵FN=PN,
∴∠NFP=∠NPF=45°,
∴∠OFP=90°,
∴四边形OFPE是矩形,
∵OF=OE,
∴四边形OFPE是正方形,
∴OF=PF=BF=1,
∴1≤b<2.




 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
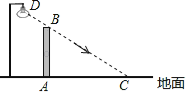
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() .以
.以![]() 为一边作等边三角形
为一边作等边三角形![]() ,点
,点![]() 在第二象限.
在第二象限.
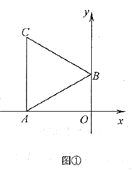
(Ⅰ)如图①,求点![]() 的坐标;
的坐标;
(Ⅱ)将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 旋转后的对应点为
旋转后的对应点为![]() .
.
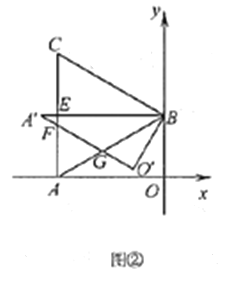
①如图②,当旋转角为30°时,![]() 与
与![]() 分别交于点
分别交于点![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 公共部分面积
公共部分面积![]() 的值;
的值;
②若![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 长的取值范围(直接写出结果即可).
长的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边
ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边![]() CDE.
CDE.
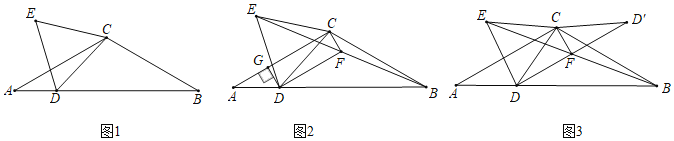
(1)如图1,若∠CDB=45°,AB=6,求等边![]() CDE的边长;
CDE的边长;
(2)如图2,点D在AB边上移动过程中,连接BE,取BE的中点F,连接CF,DF,过点D作DG⊥AC于点G.
①求证:CF⊥DF;
②如图3,将![]() CFD沿CF翻折得
CFD沿CF翻折得![]() CF
CF![]() ,连接B
,连接B![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的直径,点E是
的直径,点E是![]() 的中点,CA与
的中点,CA与![]() 相切于点A交BE延长于点C,过点A作
相切于点A交BE延长于点C,过点A作![]() 于点F,交
于点F,交![]() 于点D,交BC于点Q,连接BD.
于点D,交BC于点Q,连接BD.
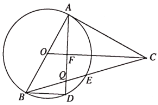
(1)求证:![]() ;
;
(2)若![]() ,求CQ的长.
,求CQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
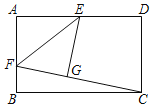
【题目】如图,矩形ABCD中,AB=8,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
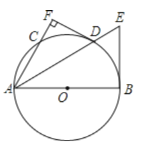
(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2.
①求![]() 值;
值;
②求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的函数表达式为
的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() 以
以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;以
;以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;以
;以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;······按此做法进行下去,其中弧
;······按此做法进行下去,其中弧![]() 的长________________.
的长________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com