
ЁОЬтФПЁПвбжЊЃЌЙигкxЕФЖўДЮКЏЪ§yЃНax2Љ2axЃЈaЃО0ЃЉЕФЖЅЕуЮЊCЃЌгыxжсНЛгкЕуOЁЂAЃЌЙигкxЕФвЛДЮКЏЪ§yЃНЉaxЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉЪдЫЕУїЕуCдквЛДЮКЏЪ§ЕФЭМЯѓЩЯЃЛ
ЃЈ2ЃЉШєСНИіЕуЃЈkЃЌy1ЃЉЁЂЃЈk+2ЃЌy2ЃЉЃЈkЁй0ЃЌЁР2ЃЉЖМдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЪЧЗёДцдкећЪ§kЃЌТњзу![]() ЃПШчЙћДцдкЃЌЧыЧѓГіkЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃПШчЙћДцдкЃЌЧыЧѓГіkЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуEЪЧЖўДЮКЏЪ§ЭМЯѓЩЯвЛЖЏЕуЃЌEЕуЕФКсзјБъЪЧnЃЌЧвЉ1ЁмnЁм1ЃЌЙ§ЕуEзїyжсЕФЦНааЯпЃЌгывЛДЮКЏЪ§ЭМЯѓНЛгкЕуFЃЌЕБ0ЃМaЁм2ЪБЃЌЧѓЯпЖЮEFЕФзюДѓжЕЃЎ
ЁОД№АИЁП(1)МћНтЮіЃЛЃЈ2ЃЉДцдкЃЎећЪ§kЕФжЕЮЊЁР4ЃЎЃЈ3ЃЉEFЕФзюДѓжЕЪЧ4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЖўДЮКЏЪ§yЃНax2Љ2axЃНaЃЈxЉ1ЃЉ2ЉaЖЅЕуCЃЈ1ЃЌЉaЃЉЃЌЕБxЃН1ЪБЃЌвЛДЮКЏЪ§жЕyЃНЉaЫљвдЕуCдквЛДЮКЏЪ§yЃНЉaxЕФЭМЯѓЩЯЃЛ
ЃЈ2ЃЉДцдкЃЎНЋЕуЃЈkЃЌy1ЃЉЁЂЃЈk+2ЃЌy2ЃЉЃЈkЁй0ЃЌЁР2ЃЉДњШыЖўДЮКЏЪ§НтЮіЪНЃЌгУaЁЂkБэЪОГіy1ЁЂy2ЃЌвђЮЊТњзу![]() ,Абy1ЁЂy2ДњШыећРэПЩЕУЙигкkЕФЗНГЬЃЌНтЗНГЬМьбщМДПЩЧѓЕУkЕФжЕ.
,Абy1ЁЂy2ДњШыећРэПЩЕУЙигкkЕФЗНГЬЃЌНтЗНГЬМьбщМДПЩЧѓЕУkЕФжЕ.
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃКЂйЕБЉ1ЁмnЁм0ЪБЃЌEFЃНyEЉyFЃНan2Љ2anЉЃЈЉanЃЉЃН![]() ЂкЕБ0ЃМnЁм1ЪБЃЌEFЃНyFЉyEЃНЉanЉЃЈan2Љ2anЃЉЃН
ЂкЕБ0ЃМnЁм1ЪБЃЌEFЃНyFЉyEЃНЉanЉЃЈan2Љ2anЃЉЃН![]()
ЃЈ1ЃЉЁпЖўДЮКЏЪ§yЃНax2Љ2axЃНaЃЈxЉ1ЃЉ2ЉaЃЌ
ЁрЖЅЕуCЃЈ1ЃЌЉaЃЉЃЌ
ЁпЕБxЃН1ЪБЃЌвЛДЮКЏЪ§жЕyЃНЉa
ЁрЕуCдквЛДЮКЏЪ§yЃНЉaxЕФЭМЯѓЩЯЃЛ
ЃЈ2ЃЉДцдкЃЎ
ЁпЕуЃЈkЃЌy1ЃЉЁЂЃЈk+2ЃЌy2ЃЉЃЈkЁй0ЃЌЁР2ЃЉЖМдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌ
Ёрy1ЃНak2Љ2akЃЌy2ЃНaЃЈk+2ЃЉ2Љ2aЃЈk+2ЃЉЃЌ
ЁпТњзу![]()
Ёр![]() ЃЌ
ЃЌ
ећРэЃЌЕУ ![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
НтЕУkЃНЁР4ЃЌ
ОМьбщЃКkЃНЁР4ЪЧдЗНГЬЕФИљЃЌ
ЁрећЪ§kЕФжЕЮЊЁР4ЃЎ
ЃЈ3ЃЉЁпЕуEЪЧЖўДЮКЏЪ§ЭМЯѓЩЯвЛЖЏЕуЃЌ
ЁрEЃЈnЃЌan2Љ2anЃЉЃЌ
ЁпEFЁЮyжсЃЌFдквЛДЮКЏЪ§ЭМЯѓЩЯЃЌЁрFЃЈnЃЌЉanЃЉЃЎ
ЂйЕБЉ1ЁмnЁм0ЪБЃЌEFЃНyEЉyFЃНan2Љ2anЉЃЈЉanЃЉЃН![]()
ЁпaЃО0ЃЌ
ЁрЕБnЃНЉ1ЪБЃЌEFгазюДѓжЕЃЌЧвзюДѓжЕЪЧ2aЃЌ
гжЁп0ЃМaЁм2ЃЌ
Ёр0ЃМ2aЁм4ЃЌМДEFЕФзюДѓжЕЪЧ4ЃЛ
ЂкЕБ0ЃМnЁм1ЪБЃЌEFЃНyFЉyEЃНЉanЉЃЈan2Љ2anЃЉЃН![]() ДЫЪБEFЕФзюДѓжЕЪЧ
ДЫЪБEFЕФзюДѓжЕЪЧ![]() ЃЌ
ЃЌ
гжЁп0ЃМaЁм2ЃЌ
Ёр0ЃМ![]() Ём
Ём![]() ЃЌМДEFЕФзюДѓжЕЪЧ
ЃЌМДEFЕФзюДѓжЕЪЧ![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌEFЕФзюДѓжЕЪЧ4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
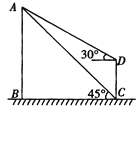
ЁОЬтФПЁПЮЊСЫВтСПФГЗчОАЧјФквЛзљЫўABЕФИпЖШЃЌФГШЫЗжБ№дкЫўЕФЖдУцвЛТЅЗПCDЕФТЅЕзCЁЂТЅЖЅDДІЃЌВтЕУЫўЖЅAЕФбіНЧЮЊ45ЁуКЭ30ЁуЃЌвбжЊТЅИпCDЮЊ10mЃЌЧѓЫўЕФИпЖШЁЃЃЈНсЙћОЋШЗЕН0ЃЎ1mЃЉЃЈВЮПМЪ§Он![]() Ёж1ЃЎ41ЃЌ
Ёж1ЃЎ41ЃЌ![]() Ёж1ЃЎ73ЃЉ
Ёж1ЃЎ73ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§СљБпаЮABCDEFЪЧБпГЄЮЊ2 cmЕФТнФИЃЌЕуPЪЧFAбгГЄЯпЩЯЕФЕуЃЌдкAЃЌPжЎМфРвЛЬѕГЄЮЊ12 cmЕФЮоЩьЫѕадЯИЯпЃЌвЛЖЫЙЬЖЈдкЕуAЃЌЮезЁСэвЛЖЫЕуPРжБЯИЯпЃЌАбЫќШЋВПНєНєВјШЦдкТнФИЩЯ(ВјШЦЪБТнФИВЛЖЏ)ЃЌдђЕуPдЫЖЏЕФТЗОЖГЄЮЊЃЈ ЃЉ
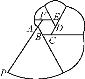
A. 13Іа cm B. 14Іа cm C. 15Іа cm D. 16Іа cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊEDЮЊЈOЕФжБОЖЧвED=4ЃЌЕуA(ВЛгыЕуEЃЌDжиКЯ)ЮЊЈOЩЯвЛИіЖЏЕуЃЌЯпЖЮABОЙ§ЕуEЃЌЧвEA=EBЃЌFЮЊЈOЩЯвЛЕуЃЌЁЯFEB=90ЁуЃЌBFЕФбгГЄЯпНЛADЕФбгГЄЯпгкЕуC.
(1)ЧѓжЄ:ЁїEFBЁеЁїADEЃЛ
(2)ЕБЕуAдкЈOЩЯвЦЖЏЪБЃЌжБНгЛиД№ЫФБпаЮFCDEЕФзюДѓУцЛ§ЮЊЖрЩй.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕЗМНЋШчЭМЫљЪОЕФШ§ЬѕЫЎЦНжБЯпm1ЃЌm2ЃЌm3ЕФЦфжавЛЬѕМЧЮЊxжсЃЈЯђгвЮЊе§ЗНЯђЃЉЃЌШ§ЬѕЪњжБжБЯпm4ЃЌm5ЃЌm6ЕФЦфжавЛЬѕМЧЮЊyжсЃЈЯђЩЯЮЊе§ЗНЯђЃЉЃЌВЂдкДЫзјБъЦНУцФкЛГіСЫХзЮяЯпy=ax2-6ax-3ЃЌдђЫ§ЫљбЁдёЕФxжсКЭyжсЗжБ№ЮЊЃЈ ЃЉ
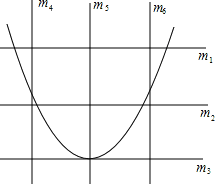
A. m1ЃЌm4 B. m2ЃЌm3 C. m3ЃЌm6 D. m4ЃЌm5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
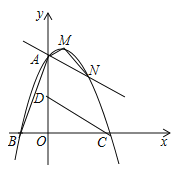
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжага![]() ЃЌ
ЃЌ![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЃЌНЋДЫШ§НЧаЮШЦдЕу
ЃЌНЋДЫШ§НЧаЮШЦдЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌЖўДЮКЏЪ§
ЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓИеКУОЙ§
ЕФЭМЯѓИеКУОЙ§![]() Ш§ЕуЃЎ
Ш§ЕуЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНМАЖЅЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЙ§ЖЈЕу![]() ЕФжБЯп
ЕФжБЯп![]() гыЖўДЮКЏЪ§ЭМЯѓЯрНЛгк
гыЖўДЮКЏЪ§ЭМЯѓЯрНЛгк![]() СНЕуЃЎ
СНЕуЃЎ
ЂйШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкжЄУїЃКЮоТл![]() ЮЊКЮжЕЃЌ
ЮЊКЮжЕЃЌ![]() КуЮЊжБНЧШ§НЧаЮЃЛ
КуЮЊжБНЧШ§НЧаЮЃЛ
ЂлЕБжБЯп![]() ШЦзХЖЈЕу
ШЦзХЖЈЕу![]() а§зЊЪБЃЌ
а§зЊЪБЃЌ![]() ЭтНгдВдВаФдквЛЬѕХзЮяЯпЩЯдЫЖЏЃЌжБНгаДГіИУХзЮяЯпЕФБэДяЪНЃЎ
ЭтНгдВдВаФдквЛЬѕХзЮяЯпЩЯдЫЖЏЃЌжБНгаДГіИУХзЮяЯпЕФБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкСтаЮABCDжаЃЌЁЯABCЃН60ЁуЃЌPЪЧЩфЯпBDЩЯвЛЖЏЕуЃЌвдAPЮЊБпЯђгвВрзїЕШБпЁїAPEЃЌСЌНгCEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуPдкСтаЮABCDФкВПЪБЃЌдђBPгыCEЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЌCEгыADЕФЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуPдкСтаЮABCDЭтВПЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыгшвджЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгBEЃЌШєABЃН2![]() ЃЌBEЃН2
ЃЌBEЃН2![]() ЃЌЧѓAPЕФГЄЃЎ
ЃЌЧѓAPЕФГЄЃЎ
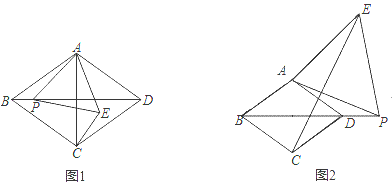
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDжаЃЌEЁЂFЗжБ№ЪЧе§ЗНаЮADЁЂCDБпЩЯЕФЕуЃЌЧвЁЯEBF=45ЁуЃЌЖдНЧЯпACНЛBE,BFгкM,NЃЌЖдгквдЯТНсТлЃЌе§ШЗЕФЪЧЃЈ ЃЉЂйAE+CF=FEЂкЁїABEЁеЁїBCFЂлAM2+CN2=MN2ЂмЁїEFDЕФжмГЄЕШгк2AB

A.ЂйЂкЂлB.ЂйЂкЂмC.ЂйЂлЂмD.ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛХњУћХЦГФЩР,ЦНОљУПЬьПЩЯњЪл20Мў,УПМўгЏРћ40дЊ.ЮЊСЫРЉДѓЯњЪл,діМггЏРћ,ОЁСПМѕЩйПтДц,ЩЬГЁОіЖЈВЩШЁЪЪЕБЕФНЕМлДыЪЉ.ОЕїВщЗЂЯж,ШчЙћУПМўГФЩРУПНЕМл5дЊ,ЩЬГЁЦНОљУПЬьПЩЖрЪлГі10Мў.Чѓ:
(1)ШєЩЬГЁУПМўГФЩРНЕМл4дЊ,дђЩЬГЁУПЬьПЩгЏРћЖрЩйдЊ?
(2)ШєЩЬГЁЦНОљУПЬьвЊгЏРћ1200дЊ,УПМўГФЩРгІНЕМлЖрЩйдЊ?
(3)вЊЪЙЩЬГЁЦНОљУПЬьгЏРћ1600дЊ,ПЩФмТ№?ЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com