
ЁОЬтФПЁПдкСтаЮABCDжаЃЌЁЯABCЃН60ЁуЃЌPЪЧЩфЯпBDЩЯвЛЖЏЕуЃЌвдAPЮЊБпЯђгвВрзїЕШБпЁїAPEЃЌСЌНгCEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуPдкСтаЮABCDФкВПЪБЃЌдђBPгыCEЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЌCEгыADЕФЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуPдкСтаЮABCDЭтВПЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыгшвджЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгBEЃЌШєABЃН2![]() ЃЌBEЃН2
ЃЌBEЃН2![]() ЃЌЧѓAPЕФГЄЃЎ
ЃЌЧѓAPЕФГЄЃЎ
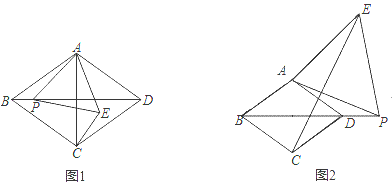
ЁОД№АИЁПЃЈ1ЃЉBP=CEЃЌCEЁЭADЃЛЃЈ2ЃЉНсТлШдШЛГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ2![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩСтаЮABCDКЭЁЯABC=60ЁуПЩжЄЁїABCгыЁїACDЪЧЕШБпШ§НЧаЮЃЌгЩЕШБпЁїAPEПЩЕУAP=AEЃЌЁЯPAE=ЁЯBAC=60ЁуЃЌМѕШЅЙЋЙВНЧЁЯPACЕУЁЯBAP=ЁЯCAEЃЌИљОнSASПЩжЄЕУЁїBAPЁеЁїCAEЃЌЙЪгаBP=CEЃЌЁЯABP=ЁЯACEЃЎгЩСтаЮЖдНЧЯпЦНЗжвЛзщЖдНЧПЩжЄЁЯABP=30ЁуЃЌЙЪЁЯACE=30ЁуМДCEЦНЗжЁЯACDЃЌгЩAC=CDЕШбќШ§НЧаЮШ§ЯпКЯвЛПЩЕУCEЁЭADЃЎ
ЃЈ2ЃЉНсТлВЛБфЃЎжЄУїЙ§ГЬЭЌЃЈ1ЃЉЃЎ
ЃЈ3ЃЉдкRtЁїAOPжаЃЌЧѓГіOAЃЌOPМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉBP=CEЃЌCEЁЭADЃЎ
РэгЩЃКЁпСтаЮABCDжаЃЌЁЯABC=60Ёу
ЁрAB=BC=CD=ADЃЌЁЯADC=ЁЯABC=60Ёу
ЁрЁїABCЁЂЁїACDЪЧЕШБпШ§НЧаЮ
ЁрAB=ACЃЌAC=CDЃЌЁЯBAC=ЁЯACD=60Ёу
ЁпЁїAPEЪЧЕШБпШ§НЧаЮ
ЁрAP=AEЃЌЁЯPAE=60Ёу
ЁрЁЯBAC-ЁЯPAC=ЁЯPAE-ЁЯPAC
МДЁЯBAP=ЁЯCAEЃЌ
ЁрЁїBAPЁеЁїCAEЃЈSASЃЉ
ЁрBP=CEЃЌЁЯABP=ЁЯACE
ЁпBDЦНЗжЁЯABC
ЁрЁЯACE=ЁЯABP=![]() ЁЯABC=30Ёу
ЁЯABC=30Ёу
ЁрCEЦНЗжЁЯACD
ЁрCEЁЭADЃЎ
ЙЪД№АИЮЊBP=CEЃЌCEЁЭADЃЎ
ЃЈ2ЃЉНсТлШдШЛГЩСЂЃЎРэгЩШчЯТЃКШчЭМЃЌЩшCEНЛADгкHЃЌСЌНгACЃЎ

ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌ
ЁрЁїABCЃЌЁїACDЖМЪЧЕШБпШ§НЧаЮЃЌЁЯABD=ЁЯCBD=30ЁуЃЎ
ЁпЁїAPEЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌAP=AEЃЌЁЯBAC=ЁЯPAE=60ЁуЃЎ
ЁрЁїBAPЁеЁїCAEЃЎ
ЁрBP=CEЃЌЁЯABP=ЁЯACE=30ЁуЃЎ
ЁпЁЯCAH=60ЁуЃЌ
ЁрЁЯCAH+ЁЯACH=90ЁуЃЎ
ЁрЁЯAHC=90ЁуЃЌМДCEЁЭADЃЎ
ЃЈ3ЃЉШчЭМЃЌСЌНгBEЃЌ

гЩЃЈ2ЃЉПЩжЊCEЁЭADЃЌBP= CEЃЎ
дкСтаЮABCDжаЃЌADЁЮBCЃЌЁрCEЁЭBCЃЎ
ЁпBC=AB=2![]() ЃЌBE=2
ЃЌBE=2![]() ЃЌ
ЃЌ
дкRtЁїBCEжаЃЌCE=![]() =8ЃЎ
=8ЃЎ
ЁрBP=CE=8ЃЎ
ЁпACгыBDЪЧСтаЮЕФЖдНЧЯпЃЌ
ЁрЁЯABD=![]() ЁЯABC=30ЁуЃЌACЁЭBDЃЎ
ЁЯABC=30ЁуЃЌACЁЭBDЃЎ
ЁрOA=![]() AB=
AB=![]() ЃЌBO=
ЃЌBO=![]() =3ЃЌ
=3ЃЌ
дкRtЁїAOPжаЃЌAP=![]() =2
=2![]() ЃЌ
ЃЌ


 бЇЖјгХЯЮНгНЬВФФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
бЇЖјгХЯЮНгНЬВФФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ аЁбЇПЮЬУзївЕЯЕСаД№АИ
аЁбЇПЮЬУзївЕЯЕСаД№АИ Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌе§ЗНаЮ
жаЃЌе§ЗНаЮ![]() жааФдкдЕуЃЌЧвЖЅЕу
жааФдкдЕуЃЌЧвЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎЖЏЕу
ЃЎЖЏЕу![]() ЗжБ№ДгЕу
ЗжБ№ДгЕу![]() ЭЌЪБГіЗЂЃЌШЦзХе§ЗНаЮЕФБпАДЫГЪБеыЗНЯђдЫЖЏЃЌЕБ
ЭЌЪБГіЗЂЃЌШЦзХе§ЗНаЮЕФБпАДЫГЪБеыЗНЯђдЫЖЏЃЌЕБ![]() ЕуЛиЕН
ЕуЛиЕН![]() ЕуЪБСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊ
ЕуЪБСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊ![]() УыЃЎСЌНг
УыЃЎСЌНг![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЁЂ
ЁЂ![]() гые§ЗНаЮЕФБпЮЇГЩЕФУцЛ§НЯаЁВПЗжЕФЭМаЮМЧЮЊ
гые§ЗНаЮЕФБпЮЇГЩЕФУцЛ§НЯаЁВПЗжЕФЭМаЮМЧЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧыаДГі![]() ЕуЕФзјБъЃЎ
ЕуЕФзјБъЃЎ
ЃЈ2ЃЉШє![]() ЕФЫйЖШОљЮЊ1ИіЕЅЮЛГЄЖШУыЃЌЪдХаЖЯдкдЫЖЏЙ§ГЬжаЃЌ
ЕФЫйЖШОљЮЊ1ИіЕЅЮЛГЄЖШУыЃЌЪдХаЖЯдкдЫЖЏЙ§ГЬжаЃЌ![]() ЕФУцЛ§ЪЧЗёЗЂЩњБфЛЏЃЌШчЙћВЛБфЧѓГіИУжЕЃЌШчЙћБфЛЏЫЕУїРэгЩЃЎ
ЕФУцЛ§ЪЧЗёЗЂЩњБфЛЏЃЌШчЙћВЛБфЧѓГіИУжЕЃЌШчЙћБфЛЏЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШє![]() ЕуЫйЖШЮЊ2ИіЕЅЮЛГЄЖШУыЃЌ
ЕуЫйЖШЮЊ2ИіЕЅЮЛГЄЖШУыЃЌ![]() ЕуЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЕБ
ЕуЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЕБ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЯТБэЃЌЗНГЬ1ЁЂЗНГЬ2ЁЂЗНГЬ3ЁЪЧАДеевЛЖЈЙцТЩХХСаЕФвЛСаЗНГЬЁЃ
ЃЈ1ЃЉВТЯыЗНГЬ1ЕФНтЃЌВЂНЋЫќУЧЕФНтЬюдкБэжаЕФПеАзДІЁЃ
ађКХ | ЗНГЬ | ЗНГЬЕФНтЃЈ |
1 |
|
|
2 |
|
|
3 |
|
|
Ё | ЁЁ | ЁЁ |
ЃЈ2ЃЉШєЗНГЬ![]()
![]() ЕФНтЪЧ
ЕФНтЪЧ![]() ЃЌВТЯыa,bЕФжЕЁЃ
ЃЌВТЯыa,bЕФжЕЁЃ
ЃЈ3ЃЉЧыаДГіетСаЗНГЬжаЕФЕкnИіЗНГЬКЭЫќЕФНтЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЙигкxЕФЖўДЮКЏЪ§yЃНax2Љ2axЃЈaЃО0ЃЉЕФЖЅЕуЮЊCЃЌгыxжсНЛгкЕуOЁЂAЃЌЙигкxЕФвЛДЮКЏЪ§yЃНЉaxЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉЪдЫЕУїЕуCдквЛДЮКЏЪ§ЕФЭМЯѓЩЯЃЛ
ЃЈ2ЃЉШєСНИіЕуЃЈkЃЌy1ЃЉЁЂЃЈk+2ЃЌy2ЃЉЃЈkЁй0ЃЌЁР2ЃЉЖМдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЪЧЗёДцдкећЪ§kЃЌТњзу![]() ЃПШчЙћДцдкЃЌЧыЧѓГіkЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃПШчЙћДцдкЃЌЧыЧѓГіkЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуEЪЧЖўДЮКЏЪ§ЭМЯѓЩЯвЛЖЏЕуЃЌEЕуЕФКсзјБъЪЧnЃЌЧвЉ1ЁмnЁм1ЃЌЙ§ЕуEзїyжсЕФЦНааЯпЃЌгывЛДЮКЏЪ§ЭМЯѓНЛгкЕуFЃЌЕБ0ЃМaЁм2ЪБЃЌЧѓЯпЖЮEFЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
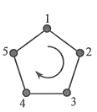
ЁОЬтФПЁПШчЭМЃЌИје§ЮхБпаЮЕФЖЅЕувРДЮБрКХ 12345ЃЌШєДгФГвЛЖЅЕуПЊЪМЃЌбие§ЮхБпаЮЕФБпЫГЪБеыаазпЃЌЖЅЕуБрКХЪ§зжЪЧМИОЭзпМИИіБпГЄЃЌдђГЦ етжжзпЗЈЮЊвЛДЮвЦЮЛЃЌШчЃКаЁгюдкБрКХЮЊ 3 ЕФЖЅЕуЩЯЪБЃЌФЧУДЫћгІИУзп 3 ИіБпГЄЃЌМД 3-4-5-1 ЮЊЕквЛДЮвЦЮЛЃЌетЪБЫћЕНДяБрКХЮЊ 1 ЕФЖЅЕуЃЛШЛКѓДг 1-2 ЮЊЕкЖўДЮвЦЮЛЃЎШєаЁгюДгБрКХЮЊ 2 ЕФЖЅЕуПЊЪМЃЌЕк 14 ДЮвЦЮЛКѓЃЌдђЫћЫљДІЖЅЕуЕФБрКХЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌгавЛзљХзЮяЯпаЮЙАЧХЃЌЧХЯТУцдке§ГЃЫЎЮЛЪБЃЌABПэ20 mЃЌЫЎЮЛЩЯЩ§ЕНОЏНфЯпCDЪБЃЌCDЕНЙАЧХЖЅEЕФОрРыНіЮЊ1 mЃЌетЪБЫЎУцПэЖШЮЊ10 m.
(1)дкШчЭМЫљЪОЕФзјБъЯЕжаЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ШєКщЫЎЕНРДЪБЃЌЫЎЮЛвдУПаЁЪБ0.3 mЕФЫйЖШЩЯЩ§ЃЌДге§ГЃЫЎЮЛПЊЪМЃЌГжајЖрЩйаЁЪБЕНДяОЏНфЯпЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
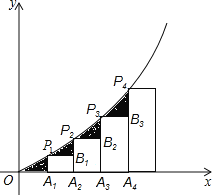
ЁОЬтФПЁПШчЭМЃЌвбжЊA1ЃЌA2ЃЌA3ЃЌЁЃЌAnЪЧxжсЩЯЕФЕуЃЌЧвOA1ЃНA1A2ЃНA2A3ЃНA3A4ЃНЁЃНAnЃ1AnЃН1ЃЌЗжБ№Й§ЕуA1ЃЌA2ЃЌA3ЃЌЁЃЌAnзїxжсЕФДЙЯпНЛЖўДЮКЏЪ§yЃН![]() x2(xЃО0)ЕФЭМЯѓгкЕуP1ЃЌP2ЃЌP3ЃЌЁЃЌPn.ШєМЧЁїOA1P1ЕФУцЛ§ЮЊS1ЃЌЙ§ЕуP1зїP1B1ЁЭA2P2гкЕуB1ЃЌМЧЁїP1B1P2ЕФУцЛ§ЮЊS2ЃЌЙ§ЕуP2зїP2B2ЁЭA3P3гкЕуB2ЃЌМЧЁїP2B2P3ЕФУцЛ§ЮЊS3ЁЁвРДЮНјааЯТШЅЃЌзюКѓМЧЁїPnЃ1BnЃ1Pn(nЃО1)ЕФУцЛ§ЮЊSnЃЌдђSnЃН(ЁЁЁЁ)
x2(xЃО0)ЕФЭМЯѓгкЕуP1ЃЌP2ЃЌP3ЃЌЁЃЌPn.ШєМЧЁїOA1P1ЕФУцЛ§ЮЊS1ЃЌЙ§ЕуP1зїP1B1ЁЭA2P2гкЕуB1ЃЌМЧЁїP1B1P2ЕФУцЛ§ЮЊS2ЃЌЙ§ЕуP2зїP2B2ЁЭA3P3гкЕуB2ЃЌМЧЁїP2B2P3ЕФУцЛ§ЮЊS3ЁЁвРДЮНјааЯТШЅЃЌзюКѓМЧЁїPnЃ1BnЃ1Pn(nЃО1)ЕФУцЛ§ЮЊSnЃЌдђSnЃН(ЁЁЁЁ)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁССЗПМфДАЛЇЕФДАСБШчЭМ1ЫљЪОЃЌЫќЪЧгЩСНИіЫФЗжжЎвЛдВзщГЩЃЈАыОЖЯрЭЌЃЉ
ЂХЧыгУДњЪ§ЪНБэЪОзАЪЮЮяЕФУцЛ§ЃК________ЃЌгУДњЪ§ЪНБэЪОДАЛЇФмЩфНјбєЙтЕФУцЛ§ЪЧ______ЃЈНсЙћБЃСєІаЃЉ
ЂЦЕБa=![]() ЃЌb=1ЪБЃЌЧѓДАЛЇФмЩфНјбєЙтЕФУцЛ§ЪЧЖрЩй?ЃЈШЁІаЁж3 ЃЉ
ЃЌb=1ЪБЃЌЧѓДАЛЇФмЩфНјбєЙтЕФУцЛ§ЪЧЖрЩй?ЃЈШЁІаЁж3 ЃЉ
ЂЧаЁССгжЩшМЦСЫШчЭМ2ЕФДАСБЃЈгЩвЛИіАыдВКЭСНИіЫФЗжжЎвЛдВзщГЩЃЌАыОЖЯрЭЌЃЉЃЌЧыФуАяЫћЫувЛЫуДЫЪБДАЛЇФмЩфНјбєЙтЕФУцЛ§ЪЧЗёИќДѓЃПШчЙћИќДѓЃЌФЧУДДѓЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
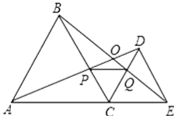
ЁОЬтФПЁПШчЭМЃЌCЮЊЯпЖЮAEЩЯвЛЖЏЕуЃЈВЛгыЕуAЃЌEжиКЯЃЉЃЌдкAEЭЌВрЗжБ№зїе§ЁїABCКЭе§ЁїCDEЃЌADгыBEНЛгкЕуOЃЌADгыBCНЛгкЕуPЃЌBEгыCDНЛгкЕуQЃЌСЌНгPQЃЎвдЯТЮхИіНсТлЃКЂйAD=BEЃЛЂкPQЁЮAEЃЛЂлAP=BQЃЛЂмCOЦНЗжЁЯAOEЃЛЂнЁЯAOB=60ЁуЃЎКуГЩСЂЕФНсТлга__ЃЎЃЈАбФуШЯЮЊе§ШЗЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com