
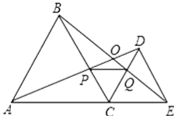
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④CO平分∠AOE;⑤∠AOB=60°.恒成立的结论有__.(把你认为正确的序号都填上)
【答案】①②③④⑤
【解析】
根据等边三角形的性质及SAS即可证明△ACD≌△BCE即可求解.
①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=120°
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=60°,CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=60°,
∴△PCQ为等边三角形,
∴∠QPC=60°=∠ACB,
∴PQ∥AE,故本选项正确;
③∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACP=∠BCQ,
∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,AP=BQ,故本选项正确;
④∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,
同理可得出∠AOE=120°,
∵D,O,C,E四点共圆,
∴∠OCD=∠OED,
∴∠OAC=∠OCD,
∴∠DCE=∠AOC=60°,
∴OC平分∠AOE,故④正确;
⑤∵△ABC、△DCE为正三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,
∵∠ACB=∠CBE+∠CEB=60°,
∴∠AOB=60°,故本选项正确.
综上所述,正确的结论是①②③④⑤.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
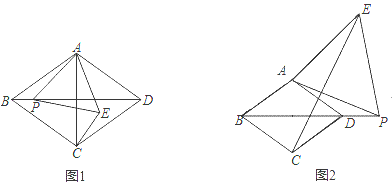
【题目】在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.
(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是 ,CE与AD的位置关系是 .
(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)如图2,连接BE,若AB=2![]() ,BE=2
,BE=2![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
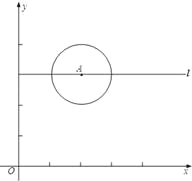
【题目】如图,已知O为坐标原点,点A的坐标为(2,3),⊙A的半径为1,过A作直线l平行于x轴,点P在l上运动.
(1)当点P运动到圆上时,求线段OP的长.
(2)当点P的坐标为(4,3)时,试判断直线OP与⊙A的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件.求:
(1)若商场每件衬衫降价4元,则商场每天可盈利多少元?
(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(3)要使商场平均每天盈利1600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式x![]() +2xy-y
+2xy-y![]() ;-x
;-x![]() -y
-y![]() +2xy;x
+2xy;x![]() +xy+y
+xy+y![]() ;4x
;4x![]() +1+4x.其中能用完全平方公式因式分解的有( )
+1+4x.其中能用完全平方公式因式分解的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com