
����Ŀ����ͼ��ֱ��y=kx+b��k��0����������y=ax2��a��0������A��B���㣬�ҵ�A�ĺ�������-2����B�ĺ�������3�������½��ۣ�
��������y=ax2��a��0����ͼ��Ķ���һ����ԭ�㣻
��x��0ʱ��ֱ��y=kx+b��k��0����������y=ax2��a��0���ĺ���ֵ������x�����������
��AB�ij��ȿ��Ե���5��
�ܡ�OAB�п��ܳ�Ϊ�ȱ������Σ�
����-3��x��2ʱ��ax2+kx��b��
������ȷ�Ľ����ǣ� ��

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
���𰸡�B
��������������������ɶ������깫ʽ�жϼ��ɣ�
������ͼ��õ�һ�κ���y=kx+bΪ�������������ߵ�x����0ʱΪ����������ѡ����ȷ��
��AB��������Ϊ5����A��B�ĺ��������ABΪ5ʱ��ֱ��AB��x��ƽ�У���k=0������֪ì�ܣ�
��������OAB������Ϊ�ȱ������Σ���ΪOA��OB��������ȣ�
��ֱ��y=-kx+b��y=kx+b����y��Գƣ������Գƺ��ͼ��y=-kx+b�������߽��������ֱ�Ϊ-3��2���ҳ�һ�κ���ͼ�����������Ϸ�ʱx�ķ�Χ�жϼ��ɣ�
�����������������y=ax2�����ö������깫ʽ�ã���������Ϊ��0��0������ѡ����ȷ��
������ͼ��ã�ֱ��y=kx+b��k��0��Ϊ��������������y=ax2��a��0����x��0ʱΪ����������x��0ʱ��ֱ���������ߺ���ֵ������x�����������ѡ����ȷ��
����A��B������ֱ�Ϊ-2��3����AB=5���ɵó�ֱ��AB��x��ƽ�У���k=0������֪k��0ì�ܣ���AB������Ϊ5����ѡ�����
����OA=OB���õ�ֱ��AB��x��ƽ�У���k=0������֪k��0ì�ܣ���OA��OB������AOB������Ϊ�ȱ������Σ���ѡ�����
��ֱ��y=-kx+b��y=kx+b����y��Գƣ���ͼ��ʾ��
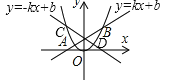
�ɵó�ֱ��y=-kx+b�������߽���C��D������ֱ�Ϊ-3��2����ͼ��ɵã���-3��x��2ʱ��ax2��-kx+b����ax2+kx��b��
����ȷ�Ľ������٢ڢ���
��ѡB��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ε��ڽǺ�Ϊ1080�㣬���������εı���Ϊ�� ��
��A��6B��7C��8D��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε����߳��ֱ�Ϊ3��6�������ߵij��Ƿ���x2��6x+8=0��һ����������������ε��ܳ��ǣ� ��
A.9
B.11
C.13
D.11��13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ���E��F�ֱ���BC��AB�ϣ���M��BA���ӳ����ϣ���CE=BF=AM������M��E�ֱ���NM��DM��NE��DE����N������NF��
��1����֤��DE��DM��
��2�����벢д���ı���CENF�������������ı��Σ���֤����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ
��1��![]()
��2���� ![]() ��2��2+
��2��2+ ![]()
��3��![]() ��
�� ![]() +
+ ![]()
��4��![]() +��1+
+��1+ ![]() ����1��
����1�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD����֪��A=90�㣬AB=3��BC=12��CD=13��DA=4�����ı��ε������ 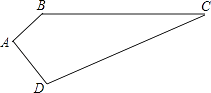
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��B��C�����������㣬OΪԭ�㣬��C��Ӧ����Ϊ3��BC=2��AB=6.
��1�����A��B��Ӧ������
��2������M��N�ֱ�ͬʱ��AC�������ֱ���ÿ��3����λ��1����λ���ٶ��������������˶�.PΪAM���е㣬Q��CN�ϣ���CQ=![]() CN�����˶�ʱ��Ϊt��t > 0��.
CN�����˶�ʱ��Ϊt��t > 0��.
�����P��Q��Ӧ�������ú�t��ʽ�ӱ�ʾ����
��tΪ��ֵʱOP=BQ.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽ���ֵ�ˮ��2010��ƽ��ÿ�����7200kg��2012��ˮ��ƽ��ÿ������IJ�����8400kg����ˮ��ÿ�����������ƽ��������Ϊx�����з���Ϊ��������
A.7200��1+x��2��8400B.7200��1+x2����8400
C.7200��x2+x����8400D.7200��1+x����8400
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com