
【题目】化简求值
(1)![]()
(2)( ![]() ﹣2)2+
﹣2)2+ ![]()
(3)![]() ﹣
﹣ ![]() +
+ ![]()
(4)![]() +(1+
+(1+ ![]() )(1﹣
)(1﹣ ![]() )
)
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】要调查下列问题,你认为哪些适合抽样调查( )
①市场上某种食品的某种添加剂的含量是否符合国家标准
②检测某地区空气质量
③调查全市中学生一天的学习时间.
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
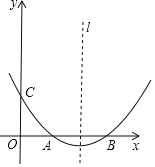
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
(1)求抛物线的解析式及A,B两点的坐标;
(2)若(1)中抛物线的对称轴上有点P,使△ABP的面积等于△ABC的面积的2倍,求出点P的坐标;
(3)在(1)中抛物线的对称轴l上是否存在一点Q,使AQ+CQ的值最小?若存在,求AQ+CQ的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承担了加工2100个机器零件的任务,甲车间单独加工了900个零件后,由于任务紧急,要求乙车间与甲车间同时加工,结果比原计划提前12天完成任务.已知乙车间的工作效率是甲车间的1.5倍,求甲、乙两车间每天加工零件各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:已知△ABC中,∠BAC=90°,AB=AC,在∠BAC内部作∠MAN=45°.AM、AN分别交BC于点M,N.
(1)将△ABM绕点A逆时针旋转90°,使AB边与AC边重合,把旋转后点M的对应点记作点Q,得到ACQ,请在图1中画出△ACQ;(不写出画法)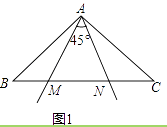
(2)在(1)中作图的基础上,连接NQ,
①求证“MN=NQ”;
②写出线段BM,MN和NC之间满足的数量关系,并简要说明理由.
(3)线段GS,ST和TH之间满足的数量关系是
(4)设DK=a,DE=b,求DP的值.(用a,b表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( ) 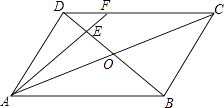
A.1:3
B.1:5
C.1:6
D.1:11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com