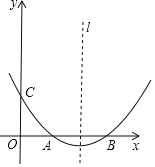
【题目】如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，﹣），且与y轴交于点C（0，2），与x轴交于A，B两点（点A在点B的左边）

（1）求抛物线的解析式及A，B两点的坐标；

（2）若（1）中抛物线的对称轴上有点P，使△ABP的面积等于△ABC的面积的2倍，求出点P的坐标；

（3）在（1）中抛物线的对称轴l上是否存在一点Q，使AQ+CQ的值最小？若存在，求AQ+CQ的最小值；若不存在，请说明理由．

参考答案：

【答案】（1）抛物线的解析式为y=（x﹣4）2﹣，A（2，0），B（6，0）；

（2）点P坐标（4，4）或（4，﹣4）；

（3）存在，QA+QC的最小值为．

【解析】（1）抛物线的顶点坐标为（4，﹣），可以假设抛物线为y=a（x﹣4）2﹣把点（0，2）代入得到a=，

∴抛物线的解析式为y=（x﹣4）2﹣．

令y=0得到（x﹣4）2﹣=0，解得x=2或6，

∴A（2，0），B（6，0）．

（2）设P（4，m），

由题意：4|m|=2××4×2，解得m=±4，

∴点P坐标（4，4）或（4，﹣4）．

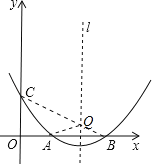
（3）存在．理由如下：

∵A、B关于对称轴对称，连接CB交对称轴于Q，连接QA，此时QA+QC最短（两点之间线段最短），

∴QA+QC的最小值=QA+QC=QB+QC=BC==．

关闭