
【题目】如图,已知一次函数![]() 的图像与x轴交于点A
的图像与x轴交于点A![]() ,交y轴于点B.
,交y轴于点B.
(1)求m的值与点B的坐标;
(2)若点C在y轴上,且使得△ABC的面积为12,请求出点C的坐标.
(3)若点P在x轴上,且△ABP为等腰三角形,请直接写出点P的坐标.

【答案】(1)![]() ,点B坐标为(0,8);(2)存在,点C坐标(0,12)或(0,4);(3)(﹣16,0),(4,0),(6,0),(
,点B坐标为(0,8);(2)存在,点C坐标(0,12)或(0,4);(3)(﹣16,0),(4,0),(6,0),(![]() ,0).
,0).
【解析】试题分析:(1)将A坐标代入一次函数解析式求出m的值,确定出一次函数解析式,令x=0求出y的值,即可确定出B的坐标;
(2)存在,理由为:设点C坐标为(0,b),表示出BC长,由三角形ABC面积以BC为底,OA为高,根据已知面积求出BC的长,确定出C坐标即可;
(3)若△ABP是等腰三角形,且点P在x轴上,分情况由等腰三角形的性质分别求得即可.
试题解析:(1)把点A(﹣6,0)代入![]() ,得m=8,∴
,得m=8,∴![]() ,
,
当x=0时,y=8,
∴点B坐标为(0,8);
(2)存在,设点C坐标为(0,b),∴BC=|8-b|,
∴![]() ×6×|8-b|=12,解得b=4或12,∴点C坐标(0,12)或(0,4);
×6×|8-b|=12,解得b=4或12,∴点C坐标(0,12)或(0,4);
(3)由题意可得AB=10,
如图,当AB=AP时,点P的坐标为(-16,0)或(4,0);
当AB=BP时,点P的坐标为(6,0);
当AP=BP时,设点P的坐标为(x,0)根据题意,得x2+82=(x+6)2,
解得x=![]() ,
,
∴点P的坐标为(![]() ,0),
,0),
综上所述,点P的坐标为(﹣16,0),(4,0),(6,0),(![]() ,0).
,0).



 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是( )
A.盈利8元B.亏损8元C.不盈不亏D.亏损15元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )



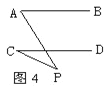
A. 、1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,∠BAD的平分线交
中,∠BAD的平分线交![]() 于E,点
于E,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() .
.
(1) 判断四边形![]() 的形状并证明;
的形状并证明;
(2) 若![]() 、
、![]() 相交于点
相交于点![]() ,且四边形
,且四边形![]() 的周长为
的周长为![]() ,
, ![]() ,求
,求![]() 的长度及四边形
的长度及四边形![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com