
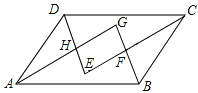
【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.

【答案】(1)证明见解析;(2)矩形;(3)![]() .
.
【解析】试题分析:(1)根据角平分线的定义以及平行四边形的性质,即可得到AB=CD,∠BAG=∠DCE,∠ABG=∠CDE,进而判定△ABG≌△CDE;
(2)根据角平分线的定义以及平行四边形的性质,即可得出∠AGB=90°,∠DEC=90°,∠AHD=90°=∠EHG,进而判定四边形EFGH是矩形;
(3)根据含30°角的直角三角形的性质,得到BG,AG,BF,CF,进而得出EF和GF的长,可得四边形EFGH的面积.
试题解析:解:(1)∵GA平分∠BAD,EC平分∠BCD,∴∠BAG=![]() ∠BAD,∠DCE=
∠BAD,∠DCE=![]() ∠DCB,∵ABCD中,∠BAD=∠DCB,AB=CD,∴∠BAG=∠DCE,同理可得,∠ABG=∠CDE,在△ABG和△CDE中,∵∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,∴△ABG≌△CDE(ASA);
∠DCB,∵ABCD中,∠BAD=∠DCB,AB=CD,∴∠BAG=∠DCE,同理可得,∠ABG=∠CDE,在△ABG和△CDE中,∵∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,∴△ABG≌△CDE(ASA);
(2)四边形EFGH是矩形.
证明:∵GA平分∠BAD,GB平分∠ABC,∴∠GAB=![]() ∠BAD,∠GBA=
∠BAD,∠GBA=![]() ∠ABC,∵ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA=
∠ABC,∵ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA=![]() (∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得,∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得,∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(3)依题意得,∠BAG=![]() ∠BAD=30°,∵AB=6,∴BG=
∠BAD=30°,∵AB=6,∴BG=![]() AB=3,AG=
AB=3,AG=![]() =CE,∵BC=4,∠BCF=
=CE,∵BC=4,∠BCF=![]() ∠BCD=30°,∴BF=
∠BCD=30°,∴BF=![]() BC=2,CF=
BC=2,CF=![]() ,∴EF=
,∴EF=![]() ﹣
﹣![]() =
=![]() ,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF=
,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF=![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】养牛场有30头大牛和15头小牛,1天用饲料675kg,一周后又购进12头大牛和5头小牛,这时1天用饲料940kg. 饲养员李大叔估计每头大牛需饲料18至21 kg,每头小牛需6至8 kg. 关于李大叔的估计,下列结论正确的是( )
A. 大牛每天所需饲料在估计的范围内,小牛每天所需饲料也在估计的范围内
B. 大牛每天所需饲料在估计的范围内,小牛每天所需饲料在估计的范围外
C. 大牛每天所需饲料在估计的范围外,小牛每天所需饲料在估计的范围内
D. 大牛每天所需饲料在估计的范围外,小牛每天所需饲料也在估计的范围外
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与x轴交于点A
的图像与x轴交于点A![]() ,交y轴于点B.
,交y轴于点B.
(1)求m的值与点B的坐标;
(2)若点C在y轴上,且使得△ABC的面积为12,请求出点C的坐标.
(3)若点P在x轴上,且△ABP为等腰三角形,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.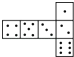 B.
B.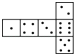 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以下现象中,属于平移的是( )
①在荡秋千的小朋友; ②电梯上升过程;
③宇宙中行星的运动; ④生产过程中传送带上的电视机的移动过程.
A.②④B.①②C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批服装.从幵始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
(1)甲车间每小时加工服装件数为 件;这批服装的总件数为 件.
(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com