
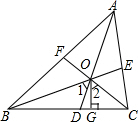
 已知,如图,点O是△ABC的三条角平分线的交点,作OG⊥BC,垂足为点G,求证:∠1=∠2.
已知,如图,点O是△ABC的三条角平分线的交点,作OG⊥BC,垂足为点G,求证:∠1=∠2. 分析 根据三条角平分线AD、BE、CF相交于点O,证明∠AOB=90°+$\frac{1}{2}$∠ACB,得到∠1=90°-$\frac{1}{2}$∠ACB,根据OC平分∠ACB,OG⊥BC,得到∠2=90°-$\frac{1}{2}$∠ACB,得到答案.
解答 证明:∵△ABC中,三条角平分线AD、BE、CF相交于点O,
∴∠OAB=$\frac{1}{2}$∠BAC,∠OBA=$\frac{1}{2}$∠ABC,
∵∠ABC+∠BAC=180°-∠BCA,
∴∠AOB=180°-(∠OAB+∠OBA)=180°-$\frac{1}{2}$(∠CAB+∠CBA)=180°-$\frac{1}{2}$(180°-∠ACB)=90°+$\frac{1}{2}$∠ACB,
∴∠1=180°-∠AOB=180°-(90°+$\frac{1}{2}$∠ACB)=90°-$\frac{1}{2}$∠ACB,
又∵OC平分∠ACB,OG⊥BC,
∴∠2=90°-$\frac{1}{2}$∠ACB,
∴∠1=∠2.
点评 此题考查了三角形内角和定理以及角平分线的定义.此题难度适中,注意掌握整体思想与数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
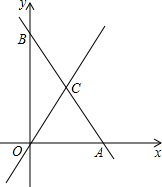 在平面直角坐标系中,直线AB的解析式为y=-2x+12,点C是线段AB的中点.
在平面直角坐标系中,直线AB的解析式为y=-2x+12,点C是线段AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
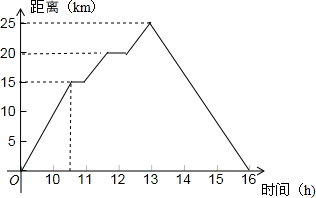 如图所示的图象,表示张同学骑车离家的距离与时间的关系,他9:00离开家,16:00到家,根据图象回答下列问题;
如图所示的图象,表示张同学骑车离家的距离与时间的关系,他9:00离开家,16:00到家,根据图象回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com