
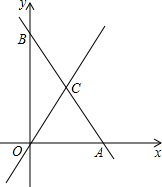
 ��ƽ��ֱ������ϵ�У�ֱ��AB�Ľ���ʽΪy=-2x+12����C���߶�AB���е㣮
��ƽ��ֱ������ϵ�У�ֱ��AB�Ľ���ʽΪy=-2x+12����C���߶�AB���е㣮���� ��1������ֱ��AB�Ľ���ʽΪy=-2x+12�����A��6��0����B��0��12�����ٸ����е����깫ʽ�õ��߶�AB���е�C������Ϊ��3��6����Ȼ�����ô���ϵ�����������ֱ��OC�Ľ���ʽ��
��2���������D�˶�����C����ʱ��Ϊ��3$\sqrt{5}$��$\sqrt{5}$=3�룬��ED��x���ڵ�M������ֱ�������ε����ʵó�OC=AC����ô��DOM=��OAB����ֱ�ǡ�DOM�����OM=OD•cos��DOM=t��DM=OD•sin��DOM=2t����D��t��2t����E��t��-2t+12�����ٷ���������������ۣ���0��t��3����t��3�����������ε������ʽ��⼴�ɣ�
��3������D�˶�ʱ��Ϊ2��ʱ��OD=2$\sqrt{5}$��D��2��4�������ô���ϵ�������ֱ��AD�Ľ���ʽΪy=-x+6���ٷ���������������ۣ���OAΪ�����εıߣ����������ε��������Q1�������Ϊ��6��6������OAΪ�����εĶԽ��ߣ�����Q2�������Ϊ��3��-3����
��� �⣺��1����ֱ��AB�Ľ���ʽΪy=-2x+12��
�൱y=0ʱ��-2x+12=0�����x=6����A��6��0����
��x=0ʱ��y=12����B��0��12����
�ߵ�C���߶�AB���е㣬
���C������3��6����
��ֱ��OC�Ľ���ʽΪy=kx��
��3k=6�����k=2��
��ֱ��OC�Ľ���ʽΪy=2x��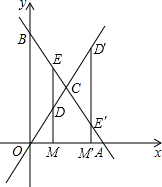 ��2����OC=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$����D�ӵ�O������������OC�����˶����ٶ�Ϊÿ��$\sqrt{5}$����λ��
��2����OC=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$����D�ӵ�O������������OC�����˶����ٶ�Ϊÿ��$\sqrt{5}$����λ��
���D�˶�����C����ʱ��Ϊ��3$\sqrt{5}$��$\sqrt{5}$=3���룩��
��ED��x���ڵ�M��
��OCΪֱ�ǡ�ABCб��AB�����ߣ�
��OC=AC��
���DOM=��OAB��
����ֱ�ǡ�DOM�У�OD=$\sqrt{5}$t��
��OM=OD•cos��DOM=OD•cos��OAB=$\sqrt{5}$t•$\frac{6}{6\sqrt{5}}$=t��
DM=OD•sin��DOM=OD•sin��OAB=$\sqrt{5}$t•$\frac{12}{6\sqrt{5}}$=2t��
��D��t��2t����
��E��t��-2t+12����
��ͼ�������������
�ٵ�0��t��3ʱ��D���߶�OC�ϣ�
��DE=-2t+12-2t=-4t+12��C��DE�ľ���Ϊ��3-t��
��S��CDE=$\frac{1}{2}$��-4t+12����3-t��=2t2-12t+18��
��S=2t2-12t+18��
�ڵ�t��3ʱ��D�߶�OC���ӳ����ϣ�
��DE=2t-��-2t+12��=4t-12��C��DE�ľ���Ϊ��t-3��
��S��CDE=$\frac{1}{2}$��4t-12����t-3��=2t2-12t+18��
��S=2t2-12t+18��
����������S��t�ĺ�����ϵʽΪS=2t2-12t+18��t��0��t��3����
��3������D�˶�ʱ��Ϊ2��ʱ��OD=2$\sqrt{5}$��D��2��4����
��ֱ��AD�Ľ���ʽΪy=mx+n��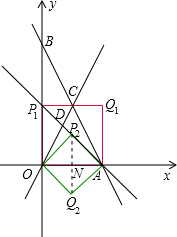 ��A��6��0����D��2��4����
��A��6��0����D��2��4����
��$\left\{\begin{array}{l}{6m+n=0}\\{2m+n=4}\end{array}\right.$�����$\left\{\begin{array}{l}{m=-1}\\{n=6}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=-x+6��
��ֱ��AD��y�ύ��Ϊ��0��6����
�Ե�O��A��P��QΪ������ı���Ϊ������ʱ�������������
�����OAΪ�����εıߣ���ͼ����������OP1Q1A����P1Ϊֱ��AD��y�ύ�㣬
��OA=OP1=6����OAQ1=90�㣬
��Q1���������6��6����
�����OAΪ�����εĶԽ��ߣ���OA�е�ΪN����N��3��0����
��x=3ʱ��y=-3+6=3��
��OA�Ĵ�ֱƽ����l����ֱ��AD�ڵ�P2��
��P2�������Ϊ��3��3������l�Ͻ�ȡNQ2=NP2��
���ı���OP2AQ2�������Σ���ʱQ2�������Ϊ��3��-3����
��������������Q�������ΪQ1��6��6����Q2��3��-3����
���� ������һ�κ����ۺ��⣬�漰�����ô���ϵ������ֱ�ߵĽ���ʽ��һ�κ���ͼ���ϵ�������������е����깫ʽ�������ε���������ɶ�����ֱ�������ε����ʣ������ε��ж������ʣ��ۺ��Խ�ǿ���Ѷ����У��������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
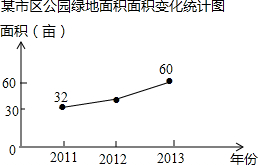 ����ij���������Ϊ180Ķ�������̻������ܱߵĻ������������Եĸ��ƣ���ͼ�Ǹù��̵�����ı仯ͳ��ͼ������2013���̵��������������2012�������ʵ�������
����ij���������Ϊ180Ķ�������̻������ܱߵĻ������������Եĸ��ƣ���ͼ�Ǹù��̵�����ı仯ͳ��ͼ������2013���̵��������������2012�������ʵ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO=CO��BO=DO���ҡ�ABC+��ADC=180�㣮
��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO=CO��BO=DO���ҡ�ABC+��ADC=180�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
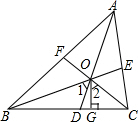 ��֪����ͼ����O�ǡ�ABC��������ƽ���ߵĽ��㣬��OG��BC������Ϊ��G����֤����1=��2��
��֪����ͼ����O�ǡ�ABC��������ƽ���ߵĽ��㣬��OG��BC������Ϊ��G����֤����1=��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com