
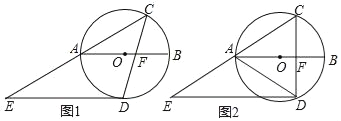
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°.点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当DE与⊙O相切时,求∠CFB的度数;
(2)如图2,当点F是CD的中点时,求△CDE的面积.
【答案】(1)75°;(2)![]() .
.
【解析】
(1)由题意可求∠AOD=90°,即可求∠C=45°,即可求∠CFB的度数;
(2)连接OC,根据垂径定理可得AB⊥CD,利用勾股定理.以及直角三角形30度性质求出CD、DE即可.
解:(1)如图:连接OD
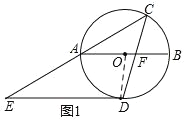
∵DE与⊙O相切
∴∠ODE=90°
∵AB∥DE
∴∠AOD+∠ODE=180°
∴∠AOD=90°
∵∠AOD=2∠C
∠C=45°
∵∠CFB=∠CAB+∠C
∴∠CFB=75°
(2)如图:连接OC

∵AB是直径,点F是CD的中点
∴AB⊥CD,CF=DF,
∵∠COF=2∠CAB=60°,
∴OF=![]() OC=
OC=![]() ,CF=
,CF=![]() OF=
OF=![]() ,
,
∴CD=2CF=![]() ,AF=OA+OF=
,AF=OA+OF=![]() ,
,
∵AF∥AD,F点为CD的中点,
∴DE⊥CD,AF为△CDE的中位线,
∴DE=2AF=3,
∴S△CED=![]() ×3×
×3×![]() =
=![]()


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10 m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
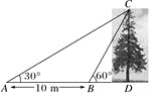
A. 10m B. 5m C. 5![]() m D. 10
m D. 10![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
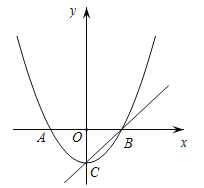
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 过顶点
过顶点![]() 和点
和点![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的解析式;
的解析式;
(3)抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
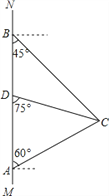
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B′和C′,使AB=![]() AB′,AC=
AB′,AC=![]() AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
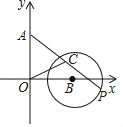
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com