
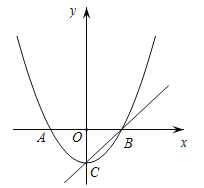
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 过顶点
过顶点![]() 和点
和点![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的解析式;
的解析式;
(3)抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)﹣3;(2)y![]() x2﹣3;(3)M的坐标为(3
x2﹣3;(3)M的坐标为(3![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).
【解析】
(1)把C(0,﹣3)代入直线y=x+m中解答即可;
(2)把y=0代入直线解析式得出点B的坐标,再利用待定系数法确定函数关系式即可;
(3)分M在BC上方和下方两种情况进行解答即可.
(1)将C(0,﹣3)代入y=x+m,可得:
m=﹣3;
(2)将y=0代入y=x﹣3得:
x=3,
所以点B的坐标为(3,0),
将(0,﹣3)、(3,0)代入y=ax2+b中,可得:
![]() ,
,
解得: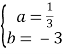 ,
,
所以二次函数的解析式为:y![]() x2﹣3;
x2﹣3;
(3)存在,分以下两种情况:

①若M在B上方,设MC交x轴于点D,
则∠ODC=45°+15°=60°,
∴OD=OCtan30°![]() ,
,
设DC为y=kx﹣3,代入(![]() ,0),可得:k
,0),可得:k![]() ,
,
联立两个方程可得: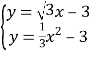 ,
,
解得: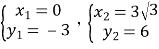 ,
,
所以M1(3![]() ,6);
,6);
②若M在B下方,设MC交x轴于点E,
则∠OEC=45°-15°=30°,
∴OE=OCtan60°=3![]() ,
,
设EC为y=kx﹣3,代入(3![]() ,0)可得:k
,0)可得:k![]() ,
,
联立两个方程可得: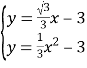 ,
,
解得: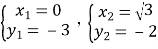 ,
,
所以M2(![]() ,﹣2).
,﹣2).
综上所述M的坐标为(3![]() ,6)或(
,6)或(![]() ,﹣2).
,﹣2).


科目:初中数学 来源: 题型:
【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
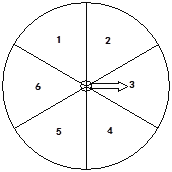
其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
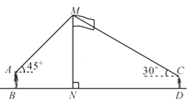
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C是线段AB上的一个动点,AB=1,分别以AC和CB为一边作正方形,用S表示这两个正方形的面积之和,下列判断正确的是( )

A. 当点C是AB的中点时,S最小 B. 当点C是AB的中点时,S最大
C. 当点C为AB的三等分点时,S最小 D. 当点C为AB的三等分点时,S最大
查看答案和解析>>
科目:初中数学 来源: 题型:
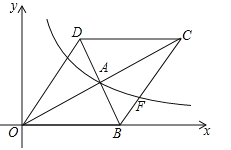
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
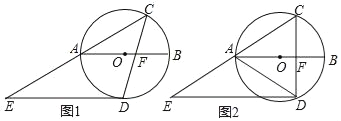
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°.点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当DE与⊙O相切时,求∠CFB的度数;
(2)如图2,当点F是CD的中点时,求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
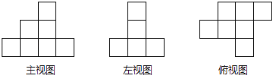
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要________个小立方块.最终搭成的长方体的表面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com