
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作等边
边上一点,作等边![]() ,连接
,连接![]() .
.
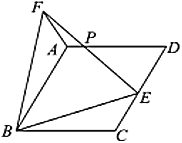
(1)求证:![]() ;
;
(2)![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)12°.
【解析】
(1)根据四边形ABCD是菱形,∠ABC=60°和等边△BEF,可以证明△FAB≌△ECB,进而可得CE=AF;
(2)利用三角形的内角和定理可求∠CBE的度数.
(1)证明:∵四边形ABCD是菱形,
∴AB=BC.
∵△BEF是等边三角形,
∴BF=BE,∠FBE=∠FEB=60°.
∵∠ABC=60°,
∴∠ABC=∠FBE,
∴∠ABC-∠ABE=∠FBE-∠ABE,即∠EBC=∠FBA.
∴△EBC≌△FBC(SAS).
∴CE=AF.
(2)解:∵四边形ABCD是菱形,
∴AD∥BC,∠D=∠ABC=60°.
∴∠C=180°-∠D=120°.
在△PDE中,∠D+∠DPE+∠PED=180°,
∴∠DEP=72°.
由(1)得,∠FEB=60°,
∴∠BED=∠DEP+∠BEP=72°+60°=132°.
∴∠CBE=∠BED-∠C=132°-120°=12°.


科目:初中数学 来源: 题型:
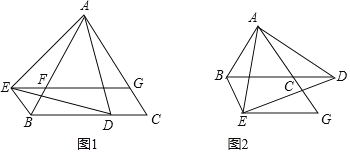
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,交射线AC于点G,连接BE.
(1)如图1所示,当点D在线段BC上时,求证:四边形BCGE是平行四边形;
(2)如图2所示,当点D在BC的延长线上时,(1)中的结论是否成立?并请说明理由;
(3)当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
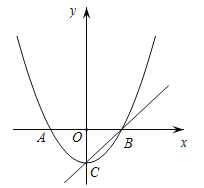
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 过顶点
过顶点![]() 和点
和点![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的解析式;
的解析式;
(3)抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )

A. 80° B. 70° C. 65° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
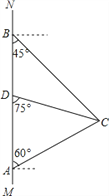
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B′和C′,使AB=![]() AB′,AC=
AB′,AC=![]() AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有 4 个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于 4”的概率.
(3)梯形ABCD中,AB∥DC,∠B=90°,E 为直线 BC上一点,若AB=5,BC=12,DC=7,当BE=?时,△ABE与△DEC相似.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com