
����Ŀ�����Ķ�����ͼ1���ı���OABC�У�OA=a��OC=3��BC=2��
��AOC=��BCO=90����������O��ֱ��l���ı��ηֳ������֣�ֱ��l��OC���ɵĽ���Ϊ�������ı���OABC��ֱ����OCB��ֱ��l�۵�����C���ڵ�D�������ǰ�����������̼�ΪFZ[�ȣ�a]��
�����⣩
����D���A�غϣ��������������ΪFZ[45�㣬3]��
�����ԣ�
��1������DǡΪAB���е㣨��ͼ2�������ȣ�
��2������FZ[45�㣬a]��������B���ڵ�E��������E���ı���OABC�ı�AB�ϣ����a��ֵ������E�����ı���OABC���ⲿ��ֱ��д��a��ȡֵ��Χ��

���𰸡���1���� =30�㣻��2����0��a��5ʱ����E�����ı���0ABC���ⲿ��
��������
��1���ȸ���ASA�����ó���BCD�ա�AFD���ʿɵó�CD=FD������DΪRt��COFб��CF���е㣬���۵���֪��OD=OC����OD=OC=CD����OCDΪ�ȱ������Σ���COD=60�㣬���ݵȱ����������ߺ�һ�����ʿɵó����ۣ���2�����ݵ�E�ı���0ABC�ı�AB�Ͽ�֪AB��ֱ��l���������۵���֪��OD=OC=3��DE=BC=2�����ɦ�=45�㣬AB��ֱ��l���ó���ADEΪ����ֱ�������Σ��ʿɵó�OA�ij����ɴ˿ɵó����ۣ�
��1������CD���ӳ�����OA�ӳ����ڵ�F��
����BCD����AFD��
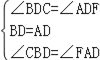 ��
��
���BCD�ա�AFD��ASA����
��CD=FD������DΪRt��COFб��CF���е㣬
��OD=![]() CF=CD��
CF=CD��
�����۵���֪��OD=OC��
��OD=OC=CD��
���OCDΪ�ȱ������Σ���COD=60�㣬
���=![]() ��COD=30�㣻
��COD=30�㣻
��2������E�ı���OABC�ı�AB�ϣ�
��AB��ֱ��l
���۵���֪��OD=OC=3��DE=BC=2��
�ߦ�=45�㣬AB��ֱ��l��
���ADEΪ����ֱ�������Σ�
��AD=DE=2��
��OA=OD+AD=3+2=5��
��a=5��
��ͼ��֪����0��a��5ʱ����E�����ı���0ABC���ⲿ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a1+a2+��+a30+a31��b1+b2+��+b30+b31��Ϊ�Ȳ�����ҽ���31���a2+b30=29��a30+b2=��9��������Ȳ���ĺ���ӵĽ��Ϊ���٣���������
A.300
B.310
C.600
D.620
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABO�У�AB��OB��OB= ![]() ��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1����Ϊ�� ��
��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1����Ϊ�� �� 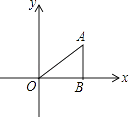
A.����1���� ![]() ��
��
B.����1���� ![]() ����2��0��
����2��0��
C.���� ![]() ��1����0����2��
��1����0����2��
D.���� ![]() ��1��
��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
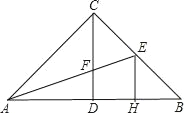
����Ŀ����ͼ������ABC�У���ACB=90������CD�ͽ�ƽ����AE���ڵ�F��EH��AB�ڵ�H����ôCF=EH��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����A=60�㣬��D���߶�BC���е㣬��EDF=120�㣬DE���߶�AB�ཻ�ڵ�E��DF���߶�AC����AC���ӳ��ߣ��ཻ�ڵ�F��
��1����ͼ1����DF��AC������ΪF��AB=4����BE�ij���
��2����ͼ2������1���еġ�EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F����֤��BE+CF= ![]() AB��
AB��
��3����ͼ3������EDF�����߷ֱ�AB��AC���ӳ�����E��F���㣬��2���еĽ��ۻ������������������֤�����������������ֱ��д���߶�BE��AB��CF֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʳƷ��ȫ�ǹغ���������Ҫ���⣬��ʳƷ�����ӹ��������Ӽ������彡���к��������������Ӽ������彡��������������ʳƷ�Ĵ�������䣮Ϊ�������������һ���о���ij���ϼӹ���������A��B�������Ϲ�100ƿ�������ͬ�����Ӽ�270�ˣ�����A����ÿƿ������Ӽ�2�ˣ�B����ÿƿ������Ӽ�3�ˣ����ϼӹ���������A��B�������ϸ�����ƿ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��ֱ�Ƕ���˳ʱ����ת90�㣬�õ���A��B��C�䣬����AA�䣬����1=22�㣬���B�Ķ����ǣ� �� 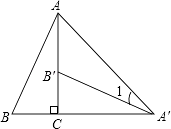
A.67��
B.62��
C.82��
D.72��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC�У�AD��BC�ڵ�D����AD= ![]() BC�����ABC�ǵĶ���Ϊ�� ��
BC�����ABC�ǵĶ���Ϊ�� ��
A.45��
B.75��
C.45���15���75��
D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�����ֽƬABCD�۵�������ʹ��ԽǶ���A��C�غϣ��������εij�BCΪ8����ABΪ4�����۵����ص����ֵ����.
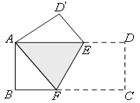
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com