Question

【题目】已知等腰△ABC中，AD⊥BC于点D，且AD= BC，则△ABC底角的度数为（ ）
A.45°
B.75°
C.45°或15°或75°
D.60°

Answer 1

【答案】C
【解析】解：①如图1，点A是顶点时，∵AB=AC，AD⊥BC，
∴BD=CD，
∵AD= BC，
∴AD=BD=CD，
在Rt△ABD中，∠B=∠BAD= （180°﹣90°）=45°；
②如图2，点A是底角顶点，且AD在△ABC外部时，
∵AD= BC，AC=BC，
∴AD= AC，
∴∠ACD=30°，
∴∠BAC=∠ABC= ×30°=15°；
③如图3，点A是底角顶点，且AD在△ABC内部时，
∵AD= BC，AC=BC，
∴AD= AC，
∴∠C=30°，
∴∠BAC=∠ABC= （180°﹣30°）=75°；
综上所述，△ABC底角的度数为45°或15°或75°．
故选C．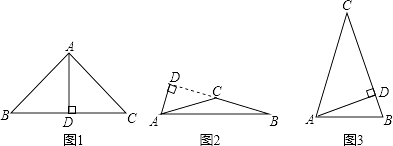

【考点精析】掌握等腰直角三角形和等腰三角形的性质是解答本题的根本，需要知道等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；等腰三角形的两个底角相等（简称：等边对等角）．