
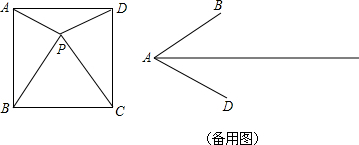
分析 (1)根据正方形的性质,利用已知条件,即可解答;
(2)正方形ABCD共有5个“准中心”;
(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;分三种情况讨论:
①如图1,当PA=PB=PC=PD时,点P是“准中心”点,
②如图2,当PA=BA=DA,PB=PC=PD时,点P是“准中心”点,
③如图3,当AB=PB=PC=PD=AD时,点P是“准中心”点,
利用角平分线的性质、等腰三角形的性质和解直角三角形,即可求出AC的长.
解答 解:(1)∵ABCD为正方形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD,
又∵∠PBC=∠PCB=60°,
∴∠BPC=60°,
∴PB=PC=BC=AB=CD,
∴PA=PD,
∴△PAB,△PBC,△PCD,△PDA均为等腰三角形,
∴点P是正方形ABCD的一个“准中心”.
(2)正方形ABCD共有5个“准中心”;
(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;
①如图1,当PA=PB=PC=PD时,点P是“准中心”点,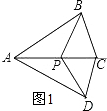
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠ACB=∠BPC=60°,∠ABC=90°,
则AC=$\frac{AB}{sin6{0}^{°}}=\frac{6}{\frac{\sqrt{3}}{2}}=4\sqrt{3}$.
②如图2,当PA=BA=DA,PB=PC=PD时,点P是“准中心”点,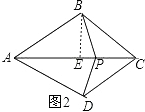
则PA=6,
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠APB=75°,
∴∠PCB=$\frac{1}{2}∠APB$=37.5°,
作BE⊥AC于点E,
在Rt△AEB中,BE=$\frac{1}{2}$AB=3,AE=AB$•cos∠BAE=3\sqrt{3}$,
在Rt△CEB中,CE=$\frac{BE}{tan∠ECB}=\frac{3}{tan37.{5}^{°}}$,
∴AC=AE+CE=$3\sqrt{3}+\frac{3}{tan37.{5}^{°}}≈9$.
③如图3,当AB=PB=PC=PD=AD时,点P是“准中心”点,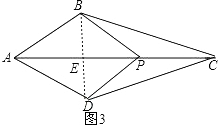
此时四边形ABPD是菱形,连接BD,
则PA=2AE=2AB•cos30°=$2×6×\frac{\sqrt{3}}{2}=6\sqrt{3}$,
∴AC=PA+PC=$6\sqrt{3}+6≈16$.
点评 本题考查了正方形的性质、等腰三角形的性质、角平分线的性质、解直角三角形,解决本题的关键是理解“准中心”的定义,结合已知条件,画出图形,再利用正方形的性质、等腰三角形的性质、角平分线的性质、解直角三角形,进行解答.在(3)中,注意分类讨论思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
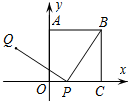 如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )
如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )| A. | 线段 | B. | 圆弧 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≥2 | B. | k≤2 | C. | -1≤k≤2 | D. | -1≤k≤2且$k≠\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.
已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).
已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com