
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D. 
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
【答案】
(1)解:∵△ABC是边长为6的等边三角形,
∴∠ACB=60°,
∵∠BQD=30°,
∴∠QPC=90°,
设AP=x,则PC=6﹣x,QB=x,
∴QC=QB+BC=6+x,
∵在Rt△QCP中,∠BQD=30°,
∴PC= ![]() QC,即6﹣x=
QC,即6﹣x= ![]() (6+x),解得x=2,
(6+x),解得x=2,
∴AP=2
(2)解:当点P、Q同时运动且速度相同时,线段DE的长度不会改变.理由如下:
作QF⊥AB,交直线AB于点F,连接QE,PF,
又∵PE⊥AB于E,
∴∠DFQ=∠AEP=90°,
∵点P、Q速度相同,
∴AP=BQ,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠FBQ=60°,
在△APE和△BQF中,
∵∠AEP=∠BFQ=90°,
∴∠APE=∠BQF,
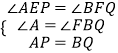 ,
,
∴△APE≌△BQF(AAS),
∴AE=BF,PE=QF且PE∥QF,
∴四边形PEQF是平行四边形,
∴DE= ![]() EF,
EF,
∵EB+AE=BE+BF=AB,
∴DE= ![]() AB,
AB,
又∵等边△ABC的边长为6,
∴DE=3,
∴点P、Q同时运动且速度相同时,线段DE的长度不会改变.
【解析】(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC= ![]() QC,即6﹣x=
QC,即6﹣x= ![]() (6+x),求出x的值即可;(2)作QF⊥AB,交直线AB于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=
(6+x),求出x的值即可;(2)作QF⊥AB,交直线AB于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE= ![]() AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.
AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形…,如此下去,则第2014个图中共有正方形的个数为( )

A. 2014. B. 2017 C. 6040 D. 6044
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数,把其十位数字与个位数字交换位置后,所得的数比原数多9,则这样的两位数的个位数字与十位数字的差是( )
A. 0B. 1C. 2D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用计算器计算时,下列说法错误的是( )
A. “计算![]() ”的按键顺序是 1 ab/c 2 ﹣ 1 ab/c 3 ab/c 4 =
”的按键顺序是 1 ab/c 2 ﹣ 1 ab/c 3 ab/c 4 =
B. “计算![]() ”的按键顺序是 3 EXP 5 ﹣ 2 8 =
”的按键顺序是 3 EXP 5 ﹣ 2 8 =
C. “已知SinA=0.3,求锐角A”的按键顺序是DEL 2ndF sin 0 . 3 =
D. “计算![]() ”的按键顺序是1 ab/c 2 2ndF
”的按键顺序是1 ab/c 2 2ndF ![]() 5 =
5 =
查看答案和解析>>
科目:初中数学 来源: 题型:
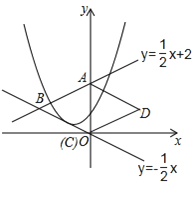
【题目】直线![]() 与
与![]() 轴交于点A,与直线
轴交于点A,与直线![]() 交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线
交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,若抛物线与菱形的边AB、BC都有公共点,则
上移动,若抛物线与菱形的边AB、BC都有公共点,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com