
【题目】如图所示,下列语句描述正确的是( )
①若∠1=∠3,则AB∥DC;②若∠C+∠1+∠4=180°,则AD∥BC;③∠A=∠C,∠ABC=∠ADC,则AB∥DC;④若∠2=∠4,BD平分∠ABC,则BC=CD;⑤若AD∥BC,∠A=∠C,则AB∥DC.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
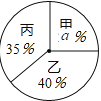
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )

A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系;
②去超市购买同一单价的水果,所付费用与水果数量的关系;
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系;
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
(1)求AP的长;
(2)求图中阴影部分的面积(结果保留π).


查看答案和解析>>
科目:初中数学 来源: 题型:
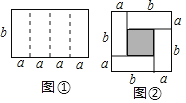
【题目】如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②)
自主探索:
(1)仔细观察图形,完成下列问题
①图②中的阴影部分的面积为_____;
②观察图②,请你写出(a+b)2、(a-b)2、ab之间的等量关系是_____;
知识运用:
(2)若x-y=5,xy=![]() ,根据(1)中的结论,求(x+y)2的值;
,根据(1)中的结论,求(x+y)2的值;
知识延伸
(3)根据你探索发现的结论,完成下列问题:
设A=![]() ,B=x+2y-3
,B=x+2y-3
计算(A-B)2-(A+B)2的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
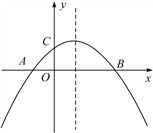
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OA·OB=-
>0;③ac-b+1=0;④OA·OB=-![]() .其中结论正确的是____________
.其中结论正确的是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y1=x+5的图象与x轴交于点A,一次函数y2=-2x+b的图象分别与x轴、y轴交于点B,C,且与y1=x+5的图象交于点D(m,4).

(1)求m,b的值;
(2)若y1>y2,则x的取值范围是 ;
(3)求四边形AOCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com