
【题目】如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)
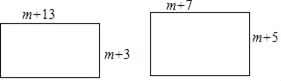
(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;
(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.
(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
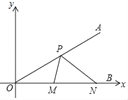
【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(6,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形组成的网格中,
的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 关于
关于![]() 轴对称的图形为
轴对称的图形为![]() .
.
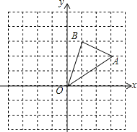
![]() 画出
画出![]() 并写出点
并写出点![]() 的坐标为________;
的坐标为________;
![]() 写出
写出![]() 的面积为________;
的面积为________;
![]() 点
点![]() 在
在![]() 轴上,使
轴上,使![]() 的值最小,写出点
的值最小,写出点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
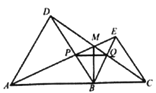
【题目】如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com