
【题目】如图,已知:![]() 的直径
的直径![]() 与弦
与弦![]() 的夹角
的夹角![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 的直径是
的直径是![]() ,以点
,以点![]() 为圆心作圆,当半径为多长时,
为圆心作圆,当半径为多长时,![]() 与
与![]() 相切?
相切?
![]() 若
若![]() ,求图中阴影部分的面积(结果精确到
,求图中阴影部分的面积(结果精确到![]() ,
,![]() )
)
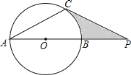
【答案】(1)见解析;(2)3;(3)4.1.
【解析】
(1)连接OC.根据圆周角定理即可求得∠COP=2∠ACO=60°,根据切线的性质定理以及直角三角形的两个锐角互余,求得∠P=30°,即可证明;
(2)如图连接BC.由圆周角定理知AC⊥BC,然后根据“AC与⊙B相切”知BC即为⊙B的半径.
(3)阴影部分的面积即为直角三角形OCP的面积减去扇形OCB的面积.
(1)如图,连接OC.
∵AO=OC,∴∠ACO=∠A=30°,∴∠COP=2∠ACO=60°.
∵PC切⊙O于点C,∴OC⊥PC.即∠OCP=90°,∴∠P=30°,∴∠A=∠P,∴AC=PC.
(2)如图,连接BC.
∵AB是⊙O的直径,∴∠ACB=90°,即AC⊥BC.
又∵AC与⊙B相切,∴BC即为⊙B的半径.
在直角△ACB中,∠A=30°,AB=6,则BC=![]() AB=3;
AB=3;
(3)在Rt△OCP中,∵∠P=30°,∴tan∠P=![]() =
=![]() ,∴OC=2
,∴OC=2![]() .
.
∵S△OCP=![]() CPOC=
CPOC=![]() ×6×2
×6×2![]() =6
=6![]() ,S扇形COB=2π,∴S阴影=S△OCP﹣S扇形COB=6
,S扇形COB=2π,∴S阴影=S△OCP﹣S扇形COB=6![]() ﹣2π≈4.1.
﹣2π≈4.1.


科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】织金县某中学300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
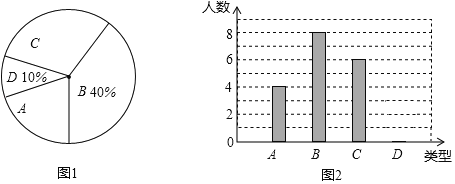
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这300名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
,![]() 是实数,定义关于“*”的一种运算:
是实数,定义关于“*”的一种运算:![]() .则下列结论正确的是( )
.则下列结论正确的是( )
①若![]() ,则
,则![]() 或
或![]() ;
;
②不存在实数![]() ,
,![]() ,满足
,满足![]() ;
;
③![]() ;
;
④若![]() ,则
,则![]() .
.
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
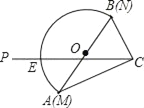
【题目】如图是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN重合,其量角器最外缘的读数是从N点开始(即N点的读数为0),现有射线CP绕着点C从CA顺时针以每秒2度的速度旋转到与△ACB外接圆相切为止.在旋转过程中,射线CP与量角器的半圆弧交于E.
(1)当射线CP与△ABC的外接圆相切时,求射线CP旋转度数是多少?
(2)当射线CP分别经过△ABC的外心、内心时,点E处的读数分别是多少?
(3)当旋转7.5秒时,连接BE,求证:BE=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com