
| A. | O | B. | 1 | C. | 2 | D. | 大于2的整数 |
分析 首先利用{x}=x-[x],将原式化简,进而由x-1<[x]≤x,得:x-1<2007x-$\frac{1}{2007}$≤x,求出[x]的值,进而得出答案.
解答 解:由题意可得:2006x+x-[x]=$\frac{1}{2007}$,
[x]=2007x-$\frac{1}{2007}$,
由x-1<[x]≤x,得:
x-1<2007x-$\frac{1}{2007}$≤x,
解得:$\frac{1}{2007×2006}$-$\frac{1}{2006}$<x≤$\frac{1}{2007×2006}$,
因此有[x]=0或-1,
当[x]=0时,
2007x=$\frac{1}{2007}$,
解得:x=($\frac{1}{2007}$)2,
当[x]=-1时,
2007x=-1+$\frac{1}{2007}$=-$\frac{2006}{2007}$,
解得:x=-$\frac{2006}{200{7}^{2}}$,
因此共有上面两个解.
故选:C.
点评 本题主要考查了取整计算以及学生对实数运算知识点的掌握,结合已知条件将原式变形转化求出取值范围为解题关键.


科目:初中数学 来源: 题型:解答题
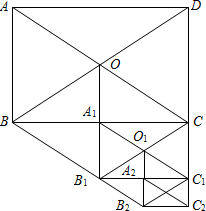 如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.
如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:
为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计.分别绘制了统计表和成绩分布直方图,请你根据统计表和成绩分布直方图回答下列问题:| 平均成绩 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | a | 3 | 3 | b | 4 | c | 6 | 1 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com