练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图所示，点A在线段CB上，AC=$\frac{1}{2}AB$，点D是线段BC的中点．若CD=3，求线段AD的长．

    分析 根据点A在线段CB上，AC=$\frac{1}{2}AB$，点D是线段BC的中点，CD=3，可以求得BC的长，从而可以求得CA的长，从而得到AD的长．

    解答 解：∵点D是线段BC的中点，CD=3，
    ∴BC=2CD=6，
    ∵AC=$\frac{1}{2}AB$，AC+AB=CB，
    ∴AC=2，AB=4，
    ∴AD=CD-AC=3-2=1，
    即线段AD的长是1．

    点评 本题考查两点间的距离，解题的关键是求出各线段的长，然后找出所问题需要的条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．在试制某种洗发液新品种时，需要选用两种不同的添加剂．现有芳香度分别为0，1，2，3，4，5的六种添加剂可供选用．根据试验设计原理，通常要先从芳香度为0，1，2的三种添加剂中随机选取一种，再从芳香度为3，4，5的三种添加剂中随机选取一种，进行搭配试验．请你利用树状图或列表的方法，表示所选取两种不同添加剂所有可能出现的结果，并求出芳香度之和等于5的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知关于x的一元二次方程（k-3）x2+3x+k2+2k-15=0的一个根为0，求k的值及方程的另一根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．方程$x+\frac{x}{1+2}+\frac{x}{1+2+3}+…+\frac{x}{1+2+…+2015}=2015$的解是x=1008．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图所示，某数学活动小组要测量山坡上的电线杆PQ的高度，他们采取的方法是：先在地面上的点A处测得杆顶端点P的仰角是45°，再向前走到B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°，这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度，你同意他们的测量方案吗？若同意，画出计算时的图形，简要写出计算的思路，不用求出具体值；若不同意，提出你的测量方案，并简要写出计算思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，为了测量某电线杆（底部可到达）的高度，准备了如下的测量工具：
    ①平面镜；②皮尺；③长为2米的标杆；④高为1.5m的测角仪（测量仰角、俯角的仪器），请根据你所设计的测量方案，回答下列问题：
    （1）画出你的测量方案示意图，并根据你的测量方案写出你所选用的测量工具；
    （2）结合你的示意图，写出求电线杆高度的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．小英、小明和小华的家都在古城东街上，小英家到小明家的距离约为300米，小明家到小华家的距离约为800米，那么小英家到小华家的距离约为1100或500米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

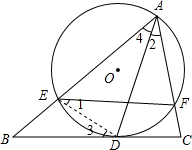    10．如图所示，AD为△ABC的角平分线，⊙O过点A，且和BC切于点D，和AB、AC分别交于E、F．如果BD=AE，BE=3，CF=2，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．符号$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$称为二阶行列式，规定它的运算法则为$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，例如：$|\begin{array}{l}{3}&{5}\\{4}&{7}\end{array}|$=3×7-4×5=21-20=1．请你根据阅读材料化简下面的二阶行列式：$|\begin{array}{l}{2a-1}&{3a+5}\\{a-5}&{2a+1}\end{array}|$，并求当a=-5时，该二阶行列式的值．

    查看答案和解析>>

    同步练习册答案