
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( ) 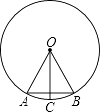
A.△OAB是等边三角形
B.弦AC的长等于圆内接正十二边形的边长
C.OC平分弦AB
D.∠BAC=30°
科目:初中数学 来源: 题型:
【题目】综合与实践:
发现问题:
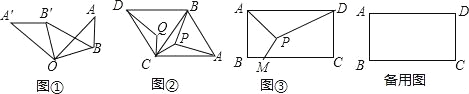
如图①,已知:△OAB中,OB=3,将△OAB绕点O逆时针旋转90°得△OA′B,连接BB′.
则BB′= .
问题探究:
如图②,已知△ABC是边长为4![]() 的等边三角形,以BC为边向外作等边△BCD,P为△ABC内一点,将线段CP绕点C逆时针旋转60°,P的对应点为Q.
的等边三角形,以BC为边向外作等边△BCD,P为△ABC内一点,将线段CP绕点C逆时针旋转60°,P的对应点为Q.
(1)求证:△DCQ≌△BCP
(2)求PA+PB+PC的最小值.
实际应用:
如图③,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A、D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B、C两点)开一个货物入口M,并修建三条专用车道PA、PD、PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系. 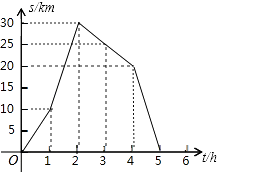
(1)在这个变化过程中自变量是 , 因变量是 .
(2)小李何时到达离家最远的地方?此时离家多远?
(3)分别求出在1≤t≤2时和2≤t≤4时小李骑自行车的速度.
(4)请直接写出小李何时与家相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年春节我市共接待国内外游客总人数3343200万人次,3343200这个数用科学记数法表示为( )
A.0.33432×106
B.3.3432×106
C.3.3432×105
D.33.432×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程4kx2﹣4kx+k+2=0的两个实数根.是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,请您说明理由.
成立?若存在,求出k的值;若不存在,请您说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com