
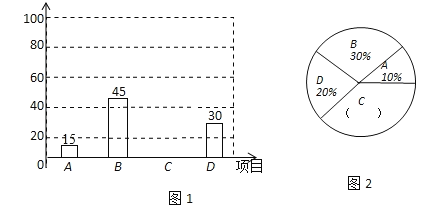
【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况,进行调查,随机抽取了部分学生,并将调查结果绘制成图1、图2的统计图,请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(3)在扇形统计图,请计算本项调查中喜欢“跑步”部分所对应的圆心角的度数;
(4)如果全校共1200名同学,请你估算喜欢“跑步”的学生人数.
【答案】(1)150名;(2)答案见解析;(3)144°;(4)480名
【解析】
(1)根据喜欢A项目的人数是15,所占的百分比是10%即可求得调查的总人数;
(2)利用总人数减去其它项的人数即可求得喜欢“跑步”的学生人数,然后根据百分比的意义求得百分比;
(3)利用360°乘以对应的百分比即可求解;
(4)利用总人数乘以对应的百分比即可.
(1)共调查了15÷10%=150名学生;
(2)本项调查中喜欢“跑步”的学生人数是;150﹣15﹣45﹣30=60(人),
所占百分比是:![]() 100%=40%,
100%=40%,
 ;
;
(3)“跑步”部分所对应的圆心角的度数是:360°×40%=144°;
(4)全校喜欢“跑步”的学生人数约是:1200×40%=480.


科目:初中数学 来源: 题型:
【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,第n个图案有 ____________个三角形(用含n的代数式表示);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
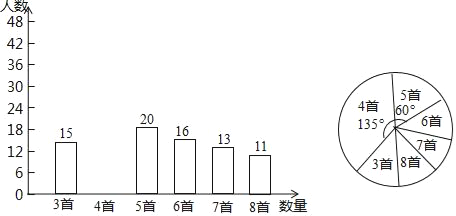
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依次剪6张正方形纸片拼成如图示意的图形,图形中正方形①的面积为1,正方形②的面积为![]() .
.
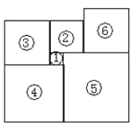
(1)请用含![]() 的式子直接写出正方形⑤的面积;
的式子直接写出正方形⑤的面积;
(2)若正方形⑥与正方形③的面积相等,求正方形④和正方形⑤的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
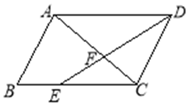
【题目】如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,若S△EFC=8,则S△CFD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
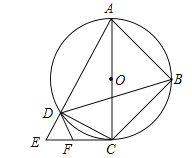
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=![]() ∶DE=4∶1,求DE的长.
∶DE=4∶1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(bc≠0).
(1)若该抛物线的顶点坐标为(c,b),求其解析式;
(2)点A(m,n),B(m+1,![]() n),C(m+6,n)在抛物线y=x2+bx+c上,求△ABC的面积;
n),C(m+6,n)在抛物线y=x2+bx+c上,求△ABC的面积;
(3)在(2)的条件下,抛物线y=x2+bx+c的图象与x轴交于D(x1,0),E(x2,0)(x1<x2)两点,且0<x1+![]() x2<3,求b的取值范围.
x2<3,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
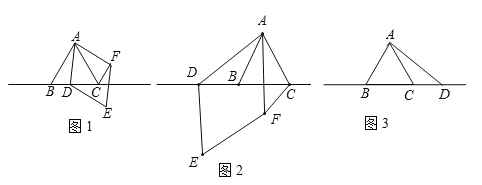
【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=![]() AB,求AG的长.
AB,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的表现较甲更稳定
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com