
【题目】已知抛物线y=x2+bx+c(bc≠0).
(1)若该抛物线的顶点坐标为(c,b),求其解析式;
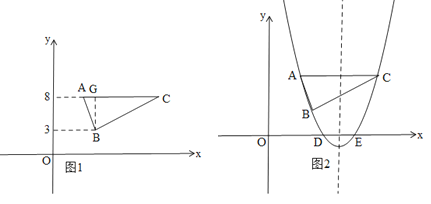
(2)点A(m,n),B(m+1,![]() n),C(m+6,n)在抛物线y=x2+bx+c上,求△ABC的面积;
n),C(m+6,n)在抛物线y=x2+bx+c上,求△ABC的面积;
(3)在(2)的条件下,抛物线y=x2+bx+c的图象与x轴交于D(x1,0),E(x2,0)(x1<x2)两点,且0<x1+![]() x2<3,求b的取值范围.
x2<3,求b的取值范围.
【答案】(1) y=x2﹣6x+3;(2)15;(3) ﹣5.5<b<﹣1且b≠﹣2.
【解析】(1)根据抛物线的顶点式和顶点坐标(c,b)设解析式,与已知的解析式列等式可求得b和c的值,写出抛物线的解析式;
(2)由A与C的纵坐标相等可得:m和m+6是方程x2+bx+c=n的两根,根据根与系数的关系列方程组可得b和c的值,把B的坐标代入抛物线的解析式中,再把b和c的值代入可得n的值,表示A、B、C三点的坐标,可求△ABC的面积;
(3)先根据(2)求出方程的两根,代入已知0<x1+![]() x2<3中,并将m换成关于b的式子,解不等式可得b的取值范围.
x2<3中,并将m换成关于b的式子,解不等式可得b的取值范围.
(1)∵抛物线的解析式为:y=x2+bx+c,∴抛物线解析式中二次顶的系数为1,设抛物线的解析式为:y=(x﹣c)2+b,∴(x﹣c)2+b=x2+bx+c,∴![]() .
.
∵bc≠0,∴![]() ,∴抛物线的解析式为:y=x2﹣6x+3;
,∴抛物线的解析式为:y=x2﹣6x+3;
(2)如图1.∵点A(m,n),C(m+6,n)在抛物线y=x2+bx+c上,∴m和m+6是方程x2+bx+c=n的两根,即x2+bx+c﹣n=0,∴![]() ,
,
解得:![]() .
.
∵B(m+1,![]() n)在抛物线y=x2+bx+c上,∴(m+1)2+b(m+1)+c=
n)在抛物线y=x2+bx+c上,∴(m+1)2+b(m+1)+c=![]() n,将b、c代入得:(m+1)2﹣2(m+3)(m+1)+m2+6m+n=
n,将b、c代入得:(m+1)2﹣2(m+3)(m+1)+m2+6m+n=![]() n,即n﹣5=
n,即n﹣5=![]() n,n=8,∴A(m,8),B(m+1,3),C(m+6,8),∴AC=6.
n,n=8,∴A(m,8),B(m+1,3),C(m+6,8),∴AC=6.
过B作BG⊥AC于G,则BG=8﹣3=5,∴S△ABC=![]() ×6×5=15;
×6×5=15;
(3)由题意得:x1+x2=﹣b=2m+6①,x1x2=c=m2+6m+8②.
∵bc≠0,∴b≠0,c≠0,∴m≠﹣2或﹣4.
∵x1<x2,由①和②得:![]() .
.
∵0<x1+![]() x2<3,∴0<3x1+x2<9,0<3(m+2)+m+4<9,0<4m+10<9.
x2<3,∴0<3x1+x2<9,0<3(m+2)+m+4<9,0<4m+10<9.
∵b=﹣2m﹣6,∴2m=﹣b﹣6.
∵m≠﹣2或﹣4,∴b≠﹣2或2,∴0<﹣2b﹣12+10<9,∴﹣5.5<b<﹣1且b≠﹣2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
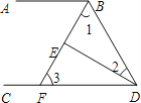
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考,完成下列填空.
问题提出:
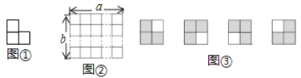
如图,图①是一张由三个边长为1的小正方形组成的![]() 形纸片.图②是张
形纸片.图②是张![]() 的方格纸(
的方格纸(![]() 的方格纸指边长分别为
的方格纸指边长分别为![]() 的长方形,被分成
的长方形,被分成![]() 个边长为1的小正方形,其中
个边长为1的小正方形,其中![]() ,且
,且![]() 为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
为正整数).把图①放置在图②中.使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
问题探究;
探究一:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,如图③,显然有4种不同的放置方法.
探究二:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在
的方格纸中,使它恰好盖住其中的三个小正方形.如图④,在![]() 的方格纸中,共可以找到2个位置不同的
的方格纸中,共可以找到2个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
的方格纸中.使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
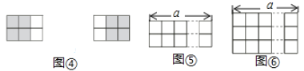
探究三:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑤,在![]() 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有________种不同的放置方法.
探究四:把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在
的方格纸中,使它恰好盖住其中的三个小正方形,如图⑥,在![]() 的方格纸中,共可以找到_______个位置不同的
的方格纸中,共可以找到_______个位置不同的![]() 方格,依据探究一的结论可知,把图①放置在
方格,依据探究一的结论可知,把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形共有________种不同的放置方法.
……
问题解决:
把图①放置在![]() 的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
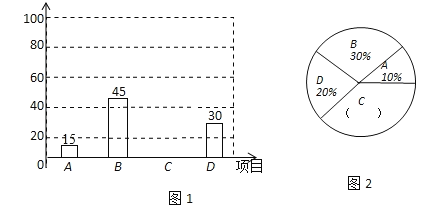
【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况,进行调查,随机抽取了部分学生,并将调查结果绘制成图1、图2的统计图,请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(3)在扇形统计图,请计算本项调查中喜欢“跑步”部分所对应的圆心角的度数;
(4)如果全校共1200名同学,请你估算喜欢“跑步”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
(1)求两人相遇时李伟离乙地的距离;
(2)请你判断:当张亮返回到甲地时,李伟是否到达乙地?

查看答案和解析>>
科目:初中数学 来源: 题型:
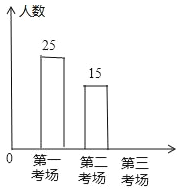
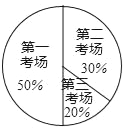
【题目】2017年12月全市组织了计算机等级考试,江南中学九(1)班同学都参加了计算机等级考试,分第一试场、第二试场、第三试场,下面两幅统计图反映原来安排九(1)班考生人数,请你根据图中的信息回答下列问题:
(1)该班参加第三试场考试的人数为_____,并补全频数分布直方图;
(2)根据实际情况,需从第一试场调部分学生到第三试场考试,使第一试场的人数与第三试场的人数比为2:3,应从第一试场调多少学生到第三试场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
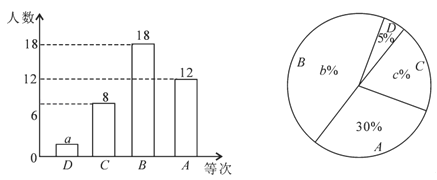
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“欢乐跑中国重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了__分钟.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com