
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 . 
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题:
解方程![]()
解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品店购进一批单件为40元的球服,如果按单价60元销售样,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单件为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
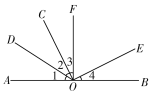
(1)∠AOC的补角是_____;
(2)____是∠AOC的余角;
(3)∠COF的补角是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足(a-![]() )2+
)2+![]() +
+![]() =0.
=0.
(1)求a,b,c的值.
(2)以a,b,c为边能否构成三角形?若能构成,求出该三角形的周长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意设未知数,并列出方程(不必求解).
(1)有两个工程队,甲队人数30名,乙队人数10名,问怎样调整两队的人数,才能使甲队的人数是乙队人数的7倍.
(2)有一个班的同学准备去划船,租了若干条船,他们计算了一下,如果比原计划多租1条船,那么正好每条船坐6人;如果比原计划少租1条船,那么正好每条船坐9人.问这个班共有多少名同学?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com