
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH丄AB于H,交AO于G,连接OH.
(1)求证:AGGO=HGGD;
(2)若AC=8,BD=6,求DG的长.

【答案】(1)见解析;(2)DG=![]()
【解析】
(1)根据菱形的性质得到AC⊥BD,由于DH⊥AB于H,于是得到∠DHA=∠DOG=90°,推出△AGH∽△DGO,根据相似三角形的性质得到![]() ,于是得到结论;
,于是得到结论;
(2)根据菱形的性质得到AO=CO=4,BO=DO=3,根据勾股定理得到AB=AD=![]() =5,根据相似三角形的性质即可得到结论.
=5,根据相似三角形的性质即可得到结论.
解:(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,AD=CD,
∴∠DAC=∠DCA,
∵DH⊥AB,
∴∠AOD=∠AHD=90°,
∵∠AGH=∠DGO,
∴△AGH∽△DGO,
∴![]()
∴AGGO=HGGD;
(2)∵四边形ABCD是菱形,AC=8,DB=6,
∴OA=![]() AC=4,OB=
AC=4,OB=![]() DB=3,
DB=3,
∴AB=![]() =5,
=5,
由(1)△AGH∽△DGO得
∠GAH=∠GDO
∵∠AOB=∠DOG=90°,
∴△AOB∽△DOG,
∴![]() ,
,
∴![]() ,
,
解得:DG=![]() .
.


科目:初中数学 来源: 题型:
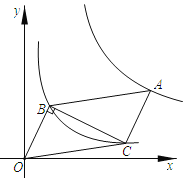
【题目】如图,在平面直角坐标系中,平行四边形ABOC的顶点B,C在反比例函数y=![]() (x>O)的图象上,点A在反比例函数y=
(x>O)的图象上,点A在反比例函数y=![]() (k>O)的图象上,若点B的坐标为(1,2),∠OBC=90°,则k的值为( )
(k>O)的图象上,若点B的坐标为(1,2),∠OBC=90°,则k的值为( )
A.![]() B.3 C.5 D.12.5
B.3 C.5 D.12.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出五年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.下图是2017年“一年一路”沿线部分国家的通信设施现状统计图.
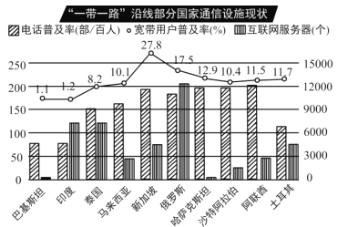
根据统计图提供的信息,下列推断合理的是( ).
A.互联网服务器拥有个数最多的国家是阿联酋
B.宽带用户普及率的中位数是11.05%
C.有8个国家的电话普及率能够达到平均每人1部
D.只有俄罗斯的三项指标均超过了相应的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 、
、![]() 的坐标.
的坐标.
(2)若直线![]() 与直线
与直线![]() 关于该抛物线的对称轴对称,该抛物线在
关于该抛物线的对称轴对称,该抛物线在![]() 这一段位于直线
这一段位于直线![]() 的上方,并且在
的上方,并且在![]() 这一段位于直线
这一段位于直线![]() 的下方,求该抛物线的解析式.
的下方,求该抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+
x2+![]() x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
(1)写出点A,B的坐标, 并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴上方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能求此时点P的坐标(直接写出结果);若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2-2mx-3m
(1)当m=1时,
①抛物线的对称轴为直线______,
②抛物线上一点P到x轴的距离为4,求点P的坐标
③当n≤x≤![]() 时,函数值y的取值范围是-
时,函数值y的取值范围是-![]() ≤y≤2-n,求n的值
≤y≤2-n,求n的值
(2)设抛物线y=x2-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y0,直接写出y0与m之间的函数关系式及m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2ax+b的顶点在x轴上,P(x1,m),Q(x2,m)(x1<x2)是此抛物线上的两点.
(1)若a=1.
①当m=b时,求x1,x2的值;
②将抛物线沿y轴平移,使得它与x轴的两个交点间的距离为4,试描述出这一变化过程;
(2)若存在实数c,使得x1≤c﹣1,且x2≥c+7成立,则m的取值范围是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com