
【题目】如图,抛物线y=![]() x2+
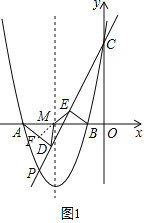
x2+![]() x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
x+4与x轴相交于点A、B与y轴相交于点C,抛物线的对称轴与x轴相交于点M,P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
(1)写出点A,B的坐标, 并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴下方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴上方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能求此时点P的坐标(直接写出结果);若不能,说明理由.

【答案】(1) A(﹣5,0),B(﹣1,0);证明见解析;(2)能;(3)(﹣![]() ,
,![]() ).
).
【解析】
(1)在抛物线解析式中,令y=0,解一元二次方程,可求得点A、点B的坐标;如图1所示,延长EM交AD于点F,证明△AMF≌△BME,得到点M为为Rt△EDF斜边EF的中点,从而得到MD=ME,问题得证;
(2)首先分析,若△MDE为等腰直角三角形,直角顶点只能是点M.如答图2所示,设直线PC与对称轴交于点N,首先证明△ADM≌△NEM,得到MN=AM,从而求得点N坐标为(﹣3,﹣2);其次利用点N、点C坐标,求出直线PC的解析式;最后联立直线PC与抛物线的解析式,求出点P的坐标.
(3)当点P是抛物线在x轴上方的一个动点时,解题思路与(2)完全相同.
解:(1)∵抛物线y=![]() x2+
x2+![]() x+4与x轴相交于点A、B两点,
x+4与x轴相交于点A、B两点,
∴令y=0,![]() ,
,
解得:x1=﹣5,x2=﹣1,
∴A(﹣5,0),B(﹣1,0).
故答案为:A(﹣5,0),B(﹣1,0).
如答图1所示,延长EM与AD交于点F.
∵AD⊥PC,BE⊥PC,
∴AD∥BE,
∴∠MAF=∠MBE.
在△AMF与△BME中,
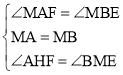 ,
,
∴△AMF≌△BME(ASA),
∴ME=MF,即点M为Rt△EDF斜边EF的中点,
∴MD=ME,
即△MDE是等腰三角形.
(2)答:能.
抛物线解析式为:![]() =
=![]() ,
,
∴对称轴是直线x=﹣3,M(﹣3,0);
令x=0,得y=4,
∴C(0,4).
△MDE为等腰直角三角形,有3种可能的情形:
①若DE⊥EM,
由DE⊥BE,可知点E、M、B在一条直线上,
而点B、M在x轴上,因此点E必然在x轴上,
由DE⊥BE,可知点E只能与点O重合,即直线PC与y轴重合,
不符合题意,故此种情况不存在;
②若DE⊥DM,与①同理可知,此种情况不存在;
③若EM⊥DM,如答图2所示:

设直线PC与对称轴交于点N,
∵EM⊥DM,MN⊥AM,
∴∠EMN=∠DMA.
在△ADM与△NEM中,

∴△ADM≌△NEM(ASA),
∴MN=MA.
∵M(﹣3,0),MN=MA=2,
∴N(﹣3,﹣2).
设直线PC解析式为y=kx+b,
∵点N(﹣3,﹣2),C(0,4)在直线上,
∴![]() ,解得k=2,b=4,
,解得k=2,b=4,
∴y=2x+4.
将y=2x+4代入抛物线解析式得:![]() ,
,
解得:x=0或![]() ,
,
当x=0时,交点为点C;
当![]() 时,y=2x+4=﹣3.
时,y=2x+4=﹣3.
∴P(![]() ,﹣3).
,﹣3).
综上所述,△MDE能成为等腰直角三角形,此时点P坐标为(![]() ,3).
,3).
(3)答:能.
与(2)同理,可知若△MDE为等腰直角三角形,直角顶点只能是点M.
∵MD⊥ME,MA⊥MN,
∴∠DMN=∠EMB.
在△DMN与△EMB中,
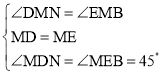 ,
,
∴△DMN≌△EMB(ASA),
∴MN=MB.
∴N(﹣3,2).
设直线PC解析式为y=kx+b,
∵点N(﹣3,2),C(0,4)在直线上,
∴![]() ,解得k=
,解得k=![]() ,b=﹣4,
,b=﹣4,
∴y=![]() x+4.
x+4.
将y=![]() x+4代入抛物线解析式得:
x+4代入抛物线解析式得:![]() x+4=
x+4=![]() x2+
x2+![]() x+4,
x+4,
解得:x=0或x=﹣![]() ,
,
当x=0时,交点为点C;当x=﹣![]() 时,y=
时,y=![]() x+4=
x+4=![]() .
.
∴P(﹣![]() ,
,![]() ).
).
综上所述,△MDE能成为等腰直角三角形,此时点P坐标为(﹣![]() ,
,![]() ).
).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,点D为半圆AB的中点,CD交AB于点E,若AC=8,BC=6,则BE的长为( )

A.4.25B.![]() C.3
C.3![]() D.4.8
D.4.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH丄AB于H,交AO于G,连接OH.
(1)求证:AGGO=HGGD;
(2)若AC=8,BD=6,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
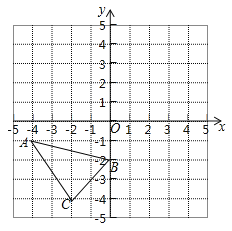
【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:2x2+6x﹣a=0.
(1)当a=5时,解方程;
(2)若2x2+6x﹣a=0的一个解是x=1,求a;
(3)若2x2+6x﹣a=0无实数解,试确定a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.
(1)从口袋中随机摸出一个小球,小球上的数字是偶数的概率是______.
(2)从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,半径OP⊥AB,过劣弧AP上一点D作DC⊥AB于点C.连接DB,交OP于点E,∠DBA=22.5°.
⑴ 若OC=2,则AC的长为 ;
⑵ 试写出AC与PE之间的数量关系,并说明理由;
⑶ 连接AD并延长,交OP的延长线于点G,设DC=x,GP=y,请求出x与y之间的等量关系式. (请先补全图形,再解答)
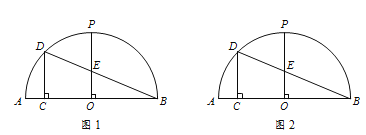
查看答案和解析>>
科目:初中数学 来源: 题型:
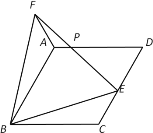
【题目】如图,在菱形ABCD中,∠ABC=60°,E是CD边上一点,作等边△BEF,连接AF.
(1)求证:CE=AF;
(2)EF与AD交于点P,∠DPE=48°,求∠CBE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com