
分析 先利用根式的性质化简,计算减法,再进一步分解因式约分化简即可.
解答 解:原式=($\frac{\sqrt{ab}}{a}$-$\frac{\sqrt{ab}}{b}$)÷($\sqrt{a}$+$\sqrt{b}$)
=$\frac{(a-b)\sqrt{ab}}{ab}$×$\frac{1}{\sqrt{a}+\sqrt{b}}$
=$\frac{\sqrt{ab}(\sqrt{a}-\sqrt{b})}{ab}$
=$\frac{a\sqrt{b}-b\sqrt{a}}{ab}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
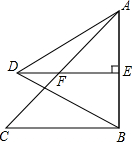 如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙0的直径,C为OA的中点,F为OB的中点,CD⊥AB交⊙0于D、EF⊥AB交⊙O于E.
如图,AB为⊙0的直径,C为OA的中点,F为OB的中点,CD⊥AB交⊙0于D、EF⊥AB交⊙O于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
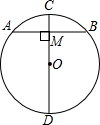 如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?
如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15° | B. | 210° | C. | 210°或30° | D. | 60°或90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com