
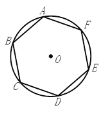
【题目】如图,六边形![]() 是⊙
是⊙![]() 的内接正六边形,若正六边形的面积等于
的内接正六边形,若正六边形的面积等于![]() ,则⊙
,则⊙![]() 的面积等于 __________ .
的面积等于 __________ .
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.
(1)若a=18cm,h=4cm,则这个无盖长方体盒子的底面面积为 ;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V= ;
(3)若a=18cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
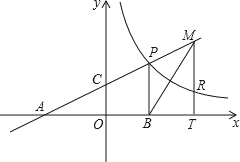
【题目】如图,直线AP的解析式y=kx+4k分别交于x轴、y轴于A、C两点,与反比例函数y=![]() (x>0)交于点P.且PB⊥x轴于B点,S△PAB=9.
(x>0)交于点P.且PB⊥x轴于B点,S△PAB=9.
(1)求一次函数解析式;
(2)点Q是x轴上的一动点,当QC+QP的值最小时,求Q点坐标;
(3)设点R与点P同在反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T点,交AC于点M,是否存在点R,使得△BTM与△AOC全等?若存在,求点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)指出下列旋转对称图形的最小旋转角,并在图中标明它的旋转中心O.
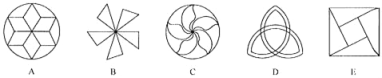
(2)在上述几个图形中有没有中心对称图形?具体指明是哪几个?
解:图形A的最小旋转角是 度,它 中心对称图形.
图形B的最小旋转角是 度,它 中心对称图形.
图形C的最小旋转角是 度,它 中心对称图形.
图形D的最小旋转角是 度,它 中心对称图形.
图形E的最小旋转角是 度,它 中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借一段墙体(墙体的最大可用长度a=10m),设AB的长为xm,所围的花圃面积为ym2,则y的最大值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .则
.则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,线段
上的射影是________点,线段![]() 在
在![]() 上的射影是___,线段
上的射影是___,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
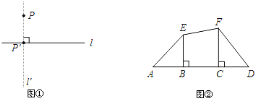
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com