
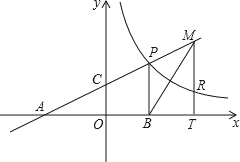
【题目】如图,直线AP的解析式y=kx+4k分别交于x轴、y轴于A、C两点,与反比例函数y=![]() (x>0)交于点P.且PB⊥x轴于B点,S△PAB=9.
(x>0)交于点P.且PB⊥x轴于B点,S△PAB=9.
(1)求一次函数解析式;
(2)点Q是x轴上的一动点,当QC+QP的值最小时,求Q点坐标;
(3)设点R与点P同在反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T点,交AC于点M,是否存在点R,使得△BTM与△AOC全等?若存在,求点R的坐标;若不存在,说明理由.
【答案】(1)直线AP解析式为y=![]() x+2;(2)Q(0.8,0);(3)R坐标为(4,1.5).
x+2;(2)Q(0.8,0);(3)R坐标为(4,1.5).
【解析】
(1)由直线AP解析式得到直线恒过A(-4,0),得到OA=4,设OB=a,PB=b,由P在反比例图象上得到ab=6,再由OA+OB表示出AB,根据AB与PB乘积的一半表示出三角形PAB面积,根据已知三角形PAB的面积求出a与b的值,确定出P坐标,将P代入直线AP解析式求出k的值即可;
(2)找出C关于x轴的对称点C′,连接PC′与x轴交于点Q,确定出直线PC′解析式,求出与x轴交点即可确定出Q坐标;
(3)由直线AP解析式求出OA与OC的长,若△BTM与△AOC全等,则有BT=OC,MT=OA,确定出M坐标,代入直线AP检验即可得到结果.
(1)直线AP解析式y=kx+4k=k(x+4),
得到A(﹣4,0),即OA=4,
设OB=a,PB=b,即P(a,b),
代入反比例解析式得:ab=6,
∵S△PAB=![]() ABPB=9,
ABPB=9,
∴![]() (a+4)b=9,即ab+4b=6+4b=18,
(a+4)b=9,即ab+4b=6+4b=18,
解得:a=2,b=3,即P(2,3),
将P(2,3)代入直线y=kx+4k中得:3=2k+4k,
解得:k=![]() ,
,
则直线AP解析式为y=![]() x+2;
x+2;
(2)对于直线y=![]() x+2,令x=0,得到y=2,即C(0,2),OC=2,
x+2,令x=0,得到y=2,即C(0,2),OC=2,
找出C关于x轴的对称点C′(0,﹣2),连接PC′,交x轴与Q点,此时QC+QP最短,
设直线C′P解析式为y=mx+n,
将P(2,3)与C′(0,﹣2)代入得:![]() ,
,
解得:m=2.5,n=﹣2,
∴直线C′P解析式为y=2.5x﹣2,
令y=0,得到x=0.8,即Q(0.8,0);
(3)若△BTM≌△COA,则有BT=OC=2,MT=OA=4,
∴OT=OB+BT=2+2=4,即M(4,4),
将x=4代入直线OP解析式得:y=![]() ×4+2=2+2=4,即M在直线AP上,
×4+2=2+2=4,即M在直线AP上,
将x=4代入反比例解析式得:y=![]() =1.5,
=1.5,
此时R坐标为(4,1.5).


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.

(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。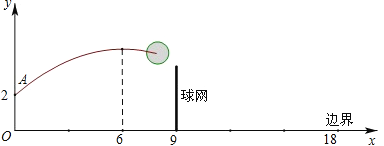
查看答案和解析>>
科目:初中数学 来源: 题型:
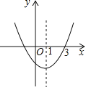
【题目】如图,二次函数![]() 的图象开口向上,对称轴为直线
的图象开口向上,对称轴为直线![]() ,图象经过
,图象经过![]() ,下列结论:①
,下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的是( )
,其中正确的是( )
A. ①②③④ B. ①③④ C. ①③ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下框中是小明对一道题目的解答以及老师的批改.
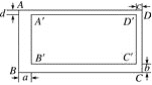
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m的空地,其他三侧内墙各保留1 m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288 m2?

解:设矩形蔬菜种植区域的宽为x_m,则长为2xm,
根据题意,得x·2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12,
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28 m,宽为14 m时,矩形蔬菜种植区域的面积是288 m2.
我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样?
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
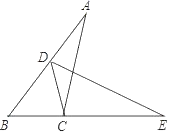
【题目】如图,已知△ABC,D是AB上一点,E是BC延长线上一点,将△ABC绕点C顺时针方向旋转,恰好能与△EDC重合.若∠A=33°,则旋转角为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
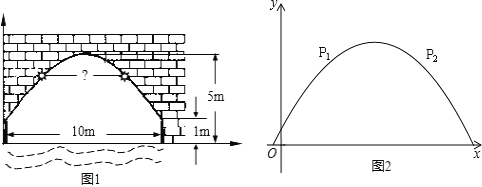
【题目】作为青岛市和李沧区的重点民生工程,经过8年不懈努力,李村河从一条城市臭水沟变成了一个美不胜收的湿地公园,因其卓越的治理效果,李村河上游综合治理工程荣获了住建部“中国人居环境范例奖”.下图是我区李村河上一座拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中.
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com