练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，抛物线y=﹣x2+2x+3与y轴交于点C，顶点为D．

    （1）求顶点D的坐标．
    （2）求△OCD的面积．

    【答案】
    （1）解：y=﹣x2+2x+3

    =﹣（x2﹣2x+1﹣1）+3

    =﹣（x﹣1）2+4，

    即顶点D的坐标为（1，4）


    （2）解：把x=0代入y=﹣x2+2x+3得：y=3，

    即OC=3，

    所以△OCD的面积为 3×1=


    【解析】（1）把解析式化成顶点式，即可得出答案；（2）求出OC的长，再根据三角形的面积公式求出即可．
    【考点精析】关于本题考查的二次函数的性质，需要了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】两枚正四面体骰子的各面上分别标有数字1，2，3，4，现在同时投掷这两枚骰子，并分别记录着地的面所得的点数为a、b．
    （1）假设两枚正四面体都是质地均匀，各面着地的可能性相同，请你在下面表格内列举出所有情形（例如（1，2），表示a=1，b=2），并求出两次着地的面点数相同的概率．

    b
    a

    1

    2

    3

    4

    1

    （1，2）

    2

    3

    4


    （2）为了验证试验用的正四面体质地是否均匀，小明和他的同学取一枚正四面体进行投掷试验．试验中标号为1的面着地的数据如下：

    试验总次数

    50

    100

    150

    200

    250

    500

    “标号1”的面着地的次数

    15

    26

    34

    48

    63

    125

    “标号1”的面着地的频率

    0.3

    0.26

    0.23

    0.24

    请完成表格（数字精确到0.01），并根据表格中的数据估计“标号1的面着地”的概率是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0），B（5，0）两点，直线y=﹣ x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

    （1）求抛物线的解析式；
    （2）若PE=5EF，求m的值；
    （3）若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，其图像如图所示，当气球内气压大于120kPa时，气球将爆炸，为了安全起见，气球内的体积应（ ）

    A. 小于1.25m3 B. 大于1.25m3 C. 不小于0.8m3 D. 大于0.8m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，边长为a的正方形发生形变后成为边长为a的菱形，如果这个菱形的一组对边之间的距离为h，我们把的值叫做这个菱形的“形变度”；例如，当形变后的菱形是如图2形状（被对角线BD分成2个等边三角形），则这个菱形的“形变度”为2：；如图3，正方形由16个边长为1的小正方形组成，形变后成为菱形，△AEF（A、E、F是格点）同时形变为△A'E'F'，若这个菱形的“形变度”k=，则_______；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角 中，∠C=90°，DC = 2，∠CAB的平分线AD交BC于点D，DE垂直平分AB．求∠B的度数和DB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC和△BOD都是等腰直角三角形，∠ACB＝∠BDO＝90°，且点A在反比例函数（k＞0）的图像上，若OB2－AB2＝10，则k的值为 （ ）

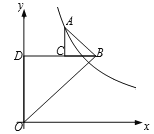
    A. 10 B. 5 C. 20 D. 2.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x，y的方程组 ，其中-3≤a≤1，给出下列结论：①当a=1时，方程组的解也是方程x＋y=4-a的解；

    ②当a=-2时，x、y的值互为相反数；

    ③若x＜1，则1≤y≤4；

    ④ 是方程组的解，其中正确的结论有

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆货车为一家摩托车配件批发部送货，先向南走了8km到达“华能”修理部，又向北走了3.5km到达“捷速”修理部，继续向北走了7.5km到达“志远”修理部，最后又回到了批发部.

    （1）以批发部为原点，以向南的方向为正方向，用1个单位长度表示1km，你能在数轴上表示出“华能”、“捷速”、“志远”三家修理部的位置吗？

    （2）“志远”修理部到“捷速”修理部多远？

    （3）货车若行驶1千米需耗油0.5升，本次这辆货车共耗油多少升？

    查看答案和解析>>

    同步练习册答案